
Tento článek jsem se rozhodl vytvořit, abych byl schopen všem vysvětlit, jak matematika ve fyzice funguje. K fyzice matematika jednoznačně patří, a proto chci, aby ji čtenář při sledování mého kurzu uměl. Průběžně budu přidávat i další články o matematice, která bude zrovna potřeba. Abych tu jen neplácal definice, pokusím se v článcích o funkcích také ukázat, k čemu je používáme při programování (to však až v příštích dílech).
První na tahu jsou tedy matematické funkce!
Dle mnoha lidí jsou funkce jednou z nejkrásnějších částí matematiky. Asi největší krásu, kterou v nich můžeme objevit, nalézáme v matematické analýze, kde rozvíjíme své znalosti, dle různých názorů, do dokonalosti.
Nejdříve bychom si ale měli říct, co to ty funkce vůbec jsou… Funkce není těžké pochopit, pokud člověk dokáže pochopit pojem „dvojice“ či „trojice“ apod. Než se ale dostaneme k tomu, co to takové funkce jsou, zkusíme se k vysvětlení logicky dopracovat – nemá totiž smysl vyřknout definici, kterou stejně nikdo nepochopí.
Dvojice a uspořádané dvojice
V matematice existuje pojem k-tice [kátice]. Mezi k-tice patří dvojice, trojice, čtveřice apod. My se zaměříme na ty nejjednodušší – dvojice. Dvojice si můžeme představit jako množiny, které obsahují dva prvky, kupříkladu množina A, která obsahuje prvky 1 a 2:
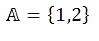
Tato dvojice je pouze jednou z mnoha milionů (nekonečna) dvojic, které existují. Pro naše vysvětlení bude stačit druhá množina B:
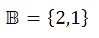
Pokud se bavíme o dvojicích, tyto jsou stejné - řekneme tedy, že dvojice A je rovna dvojici B, protože obsahuje stejné prvky a nezáleží na jejich pořadí. Pokud však chceme uspořádané dvojice, již si tyto dvojice nebudou rovny. Množina A obsahuje stejné prvky jako množina B, ale nejsou stejně uspořádané.
Matematická funkce - definice přes dvojice
Nyní se podívejme na pojem funkce. Říkáme, že funkce je množina všech uspořádaných dvojic na svém definičním oboru. Vezměme si funkci f a řekněme, že jejím definičním oborem budou přirozená čísla větší než 1. Tedy dvojice budou mít takový tvar:
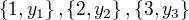
Můžeme si všimnout, že se vlastně jedná o souřadnice bodů (x a y). Souřadnici x známe a snažíme se zjistit hodnotu y. Můžeme tedy funkci zakreslit do grafu závislosti y na x. Můžeme tedy říci, že se jedná o množinu bodů v rovině.
Takto hovoříme o funkci jedné reálné proměnné, jelikož její funkční předpis je platný pouze pro x. Tímto funkčním předpisem jsme schopni nahradit právě y.
Matematická funkce - typická středoškolská definice
Obyčejně se v matematice na středních školách a gymnáziích používá definice:
Funkce je určitý matematický předpis, který jednomu x přiřazuje právě jedno y.
Všimněme si, že je to vlastně zjednodušení definice, kterou jsme si řekli u dvojic. Všechno však můžeme vztáhnout pouze na funkci jedné reálné proměnné, můžeme si ale představit i funkce více reálných proměnných – kupříkladu dvou reálných proměnných. Tyto funkce budou obsahovat x a z, bude se jednat o uspořádané trojice a bude se jednat o množinu bodů v prostoru.
Definicí pak můžeme říci, že funkce dvou reálných proměnných je předpis, který jedné uspořádané dvojici {x,z} přiřazuje právě jedno y.
Funkce jedné reálné proměnné
A jak taková funkce vypadá? Začněme funkčním předpisem. Funkčnímu předpisu (předpisu funkce) jsme v matematice přiřadili označení. V označení je vždy jméno funkce a proměnné, které v předpisu vystupují.
Pro funkci g s proměnnou n bude předpis vypadat takto: g(n).
Máme-li takový funkční předpis, jsme už schopni najít množinu bodů, která mu bude odpovídat. Funkčním předpisem může být libovolný výraz, například:
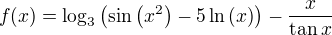
Funkce jedné reálné proměnné tedy budeme zadávat funkčním předpisem, který obsahuje x. Nemusí tomu tak být vždy, kupříkladu ve fyzice, díky které vznikl tento článek, budeme používat často funkci času, čili f(t). Pokud se bude jednat o funkci rychlosti v závislosti na čase, pak budeme funkce značit jako v(t). Stejně tak to bude i u dalších veličin, pamatujme si tedy, že písmenka jsou opravdu jen názvy a ne vždy je proměnnou x a názvem funkce f.
Každá funkce jedné reálné proměnné (dále jen funkce) má i svůj graf. Řekli jsme si, že funkce je množina bodů v rovině (souřadnice x, y), proto graf bude dvojrozměrný a bude jím buď přímka, křivka nebo jiná množina bodů, může být i nespojitá, to vše si řekneme později.
Funkci tedy můžeme zadat jak předpisem, tak grafem. Dále můžeme funkci zadat výčtem bodů, ten však nemusí být vždy přesný, jelikož dvě funkce mohou mít více stejných bodů. Abychom určili přesně danou funkci pomocí výčtu bodů, museli bychom mít všechny body, které se v ní nacházejí. Možností, jak při výčtu bodů přesně určit danou funkci, je říci, o jakou funkci se jedná (opět si vysvětlíme, jaké druhy funkcí jsou, poté určitě pochopíte, jak získat předpis pomocí dvou bodů pro přímku apod.).
Na následujícím obrázku můžeme vidět graf jedné z funkcí. Grafem je přímka, svislá je osa y, vodorovná je osa x.

Zatím jsme si řekli hodně věcí, které nejsme schopni si nijak představit, v příštích dvou článcích už si však ukážeme, jaké druhy funkcí existují a jaké jsou jejich vlastnosti. Ukážeme si také, že funkce používáme podvědomě více, než sami víme - typické ukládání hodnot do proměnné je takovou funkcí! Ale o tom až příště.
