Tentokrát se dozvíme něco málo o přímočarém pohybu. Co se bude hodit, bude určitě to, že si přiblížíme následující: přímočarý pohyb a jeho zákonitosti, nakousneme rozdíl oproti křivočarému pohybu, který probereme příště. Jestli už někdo čeká na to, že se podíváme i na „nějaké ty věci s počítačem“, tak ty nás budou čekat o kurz dál v dynamice jako dodatek k Newtonovým pohybovým rovnicím jako numerické možnosti, jak řešit libovolné diferenciální rovnice.

Dnešním tématem je tedy přímočarý pohyb. Minule jsme si ukázali obecné rovnice (pohybové rovnice) pro obecný popis libovolného pohybu. Ukažme si nyní, jak to funguje pro pohyb, který je přímočarý.

Co to vůbec je takový přímočarý pohyb?

Přímočarý pohyb je pohyb, který probíhá pouze v jednom směru. Pokud tedy budeme chtít pracovat se souřadnicemi takového bodu, můžeme soustavu souřadnou umístit tak, aby se bod pohyboval po ose x, poté nebudeme muset řešit další dvě osy, což je pro nás zajisté výhodné. Obecně tedy můžeme naše vzorce přepsat do tvaru následujícího (nenechme se zmást, že najednou pracujeme s vektory!):

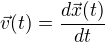
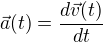
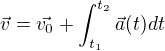
Možná bych ještě měl zmínit, ale myslím, že je to logické, že přímočarý pohyb je pohyb, jehož trajektorií je přímka; tedy množina bodů, ve kterých se bod během svého pohybu nachází, je přímka.

Rovnoměrný přímočarý pohyb

Rovnoměrný přímočarý pohyb je pohyb, kdy se hmotný bod (nebo předmět) pohybuje bez výsledného působení vnějších sil. To, jak se později dozvíme, znamená, že celkové zrychlení tělesa je rovné nule. Proto můžeme dojít k závěrům, že pohyb bude mít určité odlišnosti od ostatních pohybů. Ihned řeknu, že je nejjednodušším pohybem.

Rád bych nyní upozornil, že dost věcí, které nyní probírám, jsou i částečně vysokoškolské. Pokud jste na střední škole a prozatím nerozumíte diferenciálnímu a integrálnímu počtu (to jsou ty obecné vzorce), nemusíte se vůbec bát. Odneste si z kurzu výsledné vzorce, nemusíte je umět odvozovat, ale měli byste být schopni s nimi pracovat.

Pojďme se tedy podívat na odvození různých vlastností rovnoměrného přímočarého pohybu.

Rychlost

Okamžitou rychlost spočteme jako integrál zrychlení podle času, to již víme. Pokud je však zrychlení nulové, poté bude integrálem konstanta:

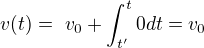
Vidíme tedy, že bez ohledu na to, jaké dva časy si vybereme, rychlost bude stále stejná, jako byla na začátku. Směr rychlosti nyní řešit nemusíme, protože víme, že je stále stejný, máme totiž nulové zrychlení. t' je pro nás vstupní čas. Mohli bychom ho psát do argumentu funkce rychlosti, ale je to pro nás částečně i zbytečné, jelikož hodnotu času t' můžeme brát za konstantu.

Změnu rychlosti na nějakém časovém úseku bychom rádi viděli nulovou. Proč? Jedná se nám o rovnoměrný pohyb, tedy pohyb, kdy je rychlost stále stejná. Můžeme se sami přesvědčit, že tento fakt opravdu platí:

Kdybychom si nechtěli hrát s úvahami a chtěli bychom definovat přímočarý rovnoměrný pohyb matematicky, použili bychom právě tyto dva vzorce, které jsme si uvedli (je to ekvivalentní s tvrzením, že zrychlení je nulové).

Poloha a dráha

Polohu bodu, ve které se bod nachází v čase t, můžeme určit velice snadno, opět si dosadíme do obecných vzorců:

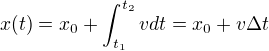
Dráhu, kterou bod urazí za určitý časový úsek, definujeme jako změnu souřadnice x bodu, jelikož jiné souřadnice se nemění.

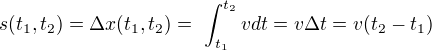
Rovnoměrně zrychlený přímočarý pohyb

Tento pohyb je pohyb, pro nějž platí, že jeho zrychlení je konstantní a po celou dobu pohybu je jeho normálová složka rovna nule.

Použijeme opět obecné vzorce jako u pohybu rovnoměrného přímočarého a dozvíme se, jak vypadá několik nových vzorců, které by správný fyzik měl znát.

Rychlost

Prvně se podívejme na rychlost v určitém čase. Počáteční čas volíme t' = 0, jen abyste věděli, proč si můžeme dovolit ze vzorců t' odebrat.

Změnu rychlosti zjistíme následujícím způsobem:

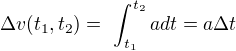
Poloha a dráha

Bez zbytečných komentářů už odvodíme následující dva vzorce pro výpočet polohy a dráhy bodu:

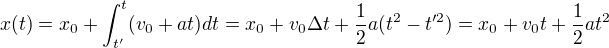
Můžeme si všimnout, že v prvním vzorci jsme elegantně mocniny t' vynechali, jelikož se rovnají nule. Proč si můžeme takovou věc dovolit? Zkoumáme, jak se bude vyvíjet poloha bodu od času t' = 0. Kdybychom použili jiný čas, zjišťovali bychom změnu polohy, k čemuž nám slouží druhý vzorec, tedy jsme neopomněli žádnou možnost, i když se na první pohled může zdát, že bychom za t' mohli dosazovat cokoliv.

Harmonický přímočarý pohyb

Harmonický pohyb je pohyb, který popisujeme pomocí harmonických funkcí sinus a kosinus. Známe matematický vztah

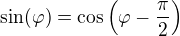
tedy víme, že je jedno, kterou funkci použijeme.

Obecný předpis polohy bodu pro harmonický přímočarý pohyb je rovnice

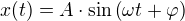
Budeme-li chtít rychlost takového pohybu, stačí nám pouze zderivovat předchozí rovnici. Zrychlení poté dostaneme opětovným zderivováním rychlosti.

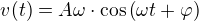
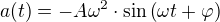
Z těchto vzorců si můžeme všimnout, že zrychlení má podobný tvar jako poloha bodu. Dokonce, pokud dáme obě rovnice do poměru a trochu zapřemýšlíme (opravdu jen minimálně :-)), dostaneme vztah

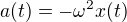
který je pro nás vcelku důležitý pro pozdější řešení pohybových rovnic v dynamice (resp. znalost tohoto vztahu nám usnadní spoustu práce).

Závěrem

Nyní již víme, jak se orientovat v přímce, víme, že nám stačí jedna souřadnice na popsání pohybu bodu či tělesa, které za bod můžeme zaměnit (v určitých případech).

Příště se podíváme na křivočaré pohyby, konkrétně plošné křivočaré pohyby a ukážeme si i případ prostorového křivočarého pohybu.

Dnes bych měl chtít úkol. Jelikož už ovládáte nějaký fyzikální aparát, tak se zeptám na vcelku jednoduchou věc.

Utíkáš před svým vrahem rychlostí 6,0 m/s a máš náskok deseti metrů. Vrah za tebou běží rychlostí 4,0 m/s. Po deseti sekundách běhu mu dojde, že mu utíkáš, proto se zastaví, dvě sekundy míří a pak vystřelí. Střela se pohybuje rychlostí 426,0 m/s. Za jak dlouho od výstřelu budeš mrtvý? (Všechny pohyby probíhají po přímce, vrah míří přesně. Působení sil, které prozatím neznáme, nebudeme uvažovat.)