Pokračování prvního dílu simulace nás zavede do oblasti matematiky. Pokusím se v něm odůvodnit metodiku simulací.

V minulém díle jsem naznačil směr, kterým by se tyto články měly ubírat a budu se jej držet. Matematice a fyzice se totiž nevyhneme. Pro začátek nám bude stačit ta matematika a později ji aplikujeme na fyzikální poznatky.

Funkce

Pro začátek drobný úvod do funkcí: funkce je předpis, kterým nějaké hodnotě přiřazujeme jinou hodnotu. Přesněji - každé hodnotě nezávislé proměnné přiřazuje právě jednu hodnotu závislé proměnné. Nezávislá proměnná bývá označována x (může to být např. i čas t), závislá je y. Setkáme se i s pojmem spojité funkce, jejíž hodnoty se mění plynule, tedy při libovolně malé změně hodnoty x se hodnota f(x) změní libovolně málo.

Po krůčcích...

V reálném světě je to podobné - čas, stejně jako všechny fyzikální pochody, jsou spojité. V případě zpracování dat v počítači ale narazíme na problém: počítač pracuje pouze s konkrétními čísly - v diskrétní oblasti! Nezná nekonečno, nedokáže zpracovávat spojité funkce. Může zpracovávat pouze vybrané okamžiky spojitého děje. Musíme tedy převést spojité děje na množinu diskrétních bodů (na obrázku jsou to body k1, k2, ...). Říkáme tomu diskretizace funkce. Po určitých intervalech nezávislé proměnné vzorkujeme výsledek (závislou proměnnou). Iterval bývá většinou konstantní, jeho velikost je rozdíl k2-k1.

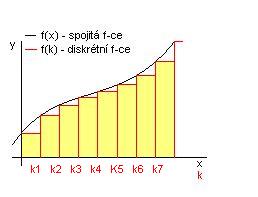
Spolu se vzorkováním se ale objevuje určitá chyba, protože nebereme v úvahu chování funkce uprostřed intervalu. Tato chyba se obvykle odstraňuje zmenšením intervalu vzorkování, ale nemůžeme jej zmenšovat donekonečna. Narážíme zde totiž na rozsah a počet čísel, které můžeme v počítači ukládat a také na časovou náročnost výpočtu.

Samá čísla

Formát čísel používaných v počítači je různý, záleží na implementaci programovacího jazyka, ale také na hardwareovém vybavení počítače. V každém případě musíme počítat s jistou nepřesností.

Známe různé celočíselné typy a čísla s pevnou nebo pohyblivou desetinnou čárkou. Dnes už bereme použití plovoucí řádové čárky za samozřejmost, ale neuvědomujeme si přitom, že pro některé počítače nebo mikropočítače je počítání ve floating point (= číslo v pohyblivé řádové čárce) časově náročné, ne-li úplně nemožné, a vždy v sobě zahrnuje určitou ztrátu dat zaokrouhlováním. Číslo se totiž ukládá ve tvaru x.xxx... Exxx, tedy jako číslo desetinné umocněné exponentem do příslušného řádu. Tímto způsobem získáme velký rozsah čísel, ale přesnost čísla je vztažená k řádu čísla. Číslo je totiž uloženo na určitý počet platných číslic, například v jazyku C (C++) je typ float interpretován devíti platnými číslicemi a typ double třinácti. Pokud tedy máme dostatek RAM a chceme zvýšit přesnost výpočtu, je rozumné používat právě typ double. Pokud bychom totiž sčítali dvě čísla s velmi rozdílným řádem, nedostali bychom správný výsledek. Stejně tak cyklické násobení řádově rozdílných hodnot se může kumulativně značně projevit a zkreslit tím výsledek. U výzkumných simulací se časová náročnost většinou zanedbává. Používají se zde výkonné víceprocesorové počítače se speciální strukturou, které zvládají i ty nejsložitější simulace s velkou přesností. Simulace se ale používá i v regulačních bezsnímačových systémech, kde je třeba počítat model regulované soustavy v reálném čase. Tam už je čas kritický a počítá se s každou mikrosekundou. Obecně platí, že příliš krátký krok simulace zvyšuje počet operací a zahlcuje paměť počítače velkým množstvím výsledků, ale zvyšuje přesnost. Obvykle jej tedy volíme jako kompromis mezi přesností a rychlostí. V laboratorních výpočtech se také často počítá záměrně s malým krokem, ale ukládá se např. každá desátá hodnota, čímž se šetří jak čas přístupu procesoru na pevný disk, tak i místo, které datový soubor zabere. Velikost kroku můžeme také bez obav určit metodou pokus-omyl (příliš pomalé nebo příliš nepřesné).

Máme na to

Samořejmě existuje celá řada programů, v kterých si můžete odsimulovat i výrobní linku, ale ne každý má v kapse sto tisíc. Takové možnosti nabízí např. MATLAB, který je komplexním a často používaným vývojovým prostředím nejen pro regulační techniku, ale i signálovou a datovou analýzu. Obsahuje kromě funkcí pro numerickou derivaci i grafické prostředí simulink, kde lze použít i různá dema k simulaci jednoduchých dějů. Různé knihovny a upgrady pak umožňují např. vizuální návrhy složitých mechanizmů i s kontrolou jejich namáhání a další možnosti pro rozličné obory lidské činnosti. V podobných cenových hladinách se pohybuje i MathCAD, který je silným zástupcem tzv. Computer Algebra Systems. Program totiž dokáže počítat v analytických rovinách. Jenže toho lze využít jen u jednoduchých idealizovaných soustav. Dojdeme tak sice k přesnému výsledku, ale nelze tu zahrnout další nelinearity a závislosti některých koeficientů (ohřívání systému, opotřebení materiálu,...), čímž se omezujeme na značně zjednodušené modely. Proto tedy saháme k principům numerické derivace a k jejímu naprogramování.

Trocha matematiky

Pokud se někdo z vás zajímal o fyziku, zjistil, že všechny dynamické děje lze definovat pomocí derivací nebo integrálů. Připomínám, že se nejedná o ekvivalentní úpravy, nelze tedy obecně zintegrováním vrátit zpět derivaci. Pro analytické řešení fyzikálních dějů se používají metody řešení diferenciálních rovnic a tzv. Cauchyho počáteční úlohy. Samozřejmě existuje i její diskrétní varianta a tou se budeme zabývat. Analyticky je derivace definovaná jako limita přírustku hodnoty závislé proměnné na přírůstek nezávislé proměnné:

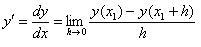
Pomocí Taylorovy řady lze dojít ke vztahu pro výpočet tohoto přírůstku bez použití limity, což už lze použít pro naše účely:

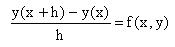
Chyba tohoto výpočtu je stejného řádu jako interval vzorkování h (neboli krok derivace).

Jak to funguje? V podstatě hledáme průběh funkce (hodnoty y v bodě x+h), který ale v každém okamžiku závisí na předcházejícím stavu (hodnotě y v bodě x). V simulaci pak využijeme toho, že mnoho dějů je popsaných právě diferenciálními rovnicemi, takže naším jediným problémem bude sestavit matematický model a ten následně naprogramovat. Na následujícím obrázku je typický průběh veličiny jednoduchého dynamického děje. Pokud bychom uvažovali funkci rychlosti v čase, např. pohyb nafukovacího balónku, dal by se děj popsat takto: udeříme do balónku a ten se začne pohybovat určitou rychlostí, kterou jsme mu udělili. Jenže v pohybu mu brání odpor vzduchu, který je ale závislý na okamžité rychlosti balónku. Díky tomu se rychlost balónku nemění po přímce (lineárně).

Jak bylo popsáno v předcházejícím díle, nejsme schopni na počítači spočítat okamžiky bezprostředně po sobě následující, jen po určitém kroku. Jedinou hodnotu, kterou máme k dispozici, je hodnota na počátku děje a potom vždy hodnota z předcházejícího výpočtového kroku. Uvedené vzorce tedy upravíme do kýžené podoby:

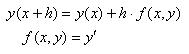
Tyto rovnice (Eulerova metoda) už nahrávají programátorovi. Vzorec nám totiž říká: pokud známe předcházející stav (v okamžiku x), můžeme vypočítat stav bezprostředně následující (x+h). Samozřejmě musíme znát i fyzikální podstatu děje vyjádřenou derivací y', neboli f(x,y). K serióznímu výpočtu nám tedy chybí už jen ten počáteční stav systému (počáteční podmínky - proto Cauchyho počáteční úloha). Ten si můžeme sami určit. Obvykle nás zajímá uvedení systému z klidu do nějakého provozního stavu (potom bývají počáteční podmínky nulové) nebo z provozního stavu do nějakého krajního až havarijního stavu (počáteční podmínky zde odpovídají ustálenému provoznímu stavu).

Čas je pánem...

Většina simulací v domácích podmínkách bývá závislá na čase. Vyplývá to z charakteru našich zájmů - činností v čase: rozběh motoru, start zdroje napětí, plnění záchodového splachovače vodou :) ... Samozřejmě lze zvolit i jinou nezávislou proměnnou. Jde pouze o jinou interpretaci fyzikálního děje. Může nás třeba zajímat změna odporu na teplotě nebo mechanické napětí v nosníku při jeho zatížení. Výsledkem potom ale nebývají časové funkce, ale funkce jiných veličin. Lze se takto dopracovat k různým důležitým charakteristikám.

V příštím díle si ukážeme, jak fyzikální děj vmontovat do našich rovnic pro numerickou podobu Cauchyho počáteční úlohy