
Poslední sada úloh letošního Google Code Jam [ http://code.google.com/codejam/ ] byla zadaná ve finále [ http://code.google.com/codejam/contest/dashboard?c=agdjb2RlamFtchALEghjb250ZXN0cxjRzBQM ]. Některé úlohy jsou již obtížnější, ale jiné se stále soustředí spíše na rychlé vymyšlení jednoduchého algoritmu. Na stránkách soutěže se také objevil oficiální klíč k řešení všech dosud zveřejněných soutěžních úloh, kde lze najít podrobnější vysvětlení řešení problémů.
Džus
Zadání: Na párty jsme pozvali daný počet lidí. Každý z těchto lidí má rád džus namíchaný z přísad A, B a C. Problém je, že každému vyhovuje jiné množství těchto přísad. Naším úkolem je stanovit takové množství přísad, abychom uspokojili co nejvíc lidí. U každého člověka máme zadáno, kolik které přísady minimálně chce, aby mu džus chutnal (maximální součet přísad je stanoven jako číslo 10 000). Řešení [ #finals-a ]
Řešení: U dvou přísad by se dalo postupovat tak, že bychom si do pole $plusminus u každého člověka poznamenali, od jakého do jakého množství jedné přísady mu džus bude chutnat. V tomto poli bychom pak hledali maximální hodnotu. Pro tři přísady stačí vyzkoušet sestavit toto pole pro všechny možné hodnoty třetí přísady.
function juices($people) {
$return = 0;
sort($people);
foreach (array_reverse($people, true) as $key => $val) {
list($a, $b, $c) = $val;
$plusminus = array();
foreach ($people as $val2) {
list($a2, $b2, $c2) = $val2;
if ($a + $b2 + $c2 <= 10000) {
$plusminus[$b2]++;
$plusminus[10001 - $a - $c2] -= 1;
}
}
ksort($plusminus);
$value = 0;
foreach ($plusminus as $val) {
$value += $val;
$return = max($return, $value);
}
unset($people[$key]);
}
return $return;
}Pro dekrementaci pole $plusminus se nepoužívá operátor --, ale konstrukce -= 1. Důvodem je, že hodnotu null operátor -- nesníží.
Pingpongové balónky
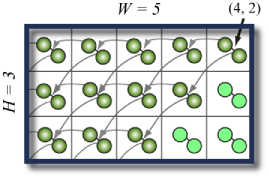 Zadání: Ve veliké místnosti zadaných rozměrů jsou na všech políčcích totožné pasti na myši. Každá past je nabita dvěma balónky, které se při aktivaci vystřelí na relativně zadané políčko a aktivují past, která na cílovém políčku leží. Naším úkolem je zjistit, kolik pastí se celkem aktivuje, pokud jako první aktivujeme past na určeném políčku. Řešení [ #finals-b ]
Zadání: Ve veliké místnosti zadaných rozměrů jsou na všech políčcích totožné pasti na myši. Každá past je nabita dvěma balónky, které se při aktivaci vystřelí na relativně zadané políčko a aktivují past, která na cílovém políčku leží. Naším úkolem je zjistit, kolik pastí se celkem aktivuje, pokud jako první aktivujeme past na určeném políčku. Řešení [ #finals-b ]
Řešení: Funkce začne na startovním políčku a ověří, jestli balónek ještě nevypadl z místnosti a jestli jsme dané políčko už nenavštívili. Pokud ne, tak nejprve aktivuje jeden balónek a potom druhý.
function pingpong($size, $ball1, $ball2, $x, $y, &$hits = array()) {
if ($x >= 0 && $x < $size[0] && $y >= 0 && $y < $size[1] && !isset($hits["$x:$y"])) {
$hits["$x:$y"] = true;
pingpong($size, $ball1, $ball2, $x + $ball1[0], $y + $ball1[1], $hits);
pingpong($size, $ball1, $ball2, $x + $ball2[0], $y + $ball2[1], $hits);
}
return count($hits);
}Pro vyřešení velkého vstupu by bylo potřeba zjistit, do jakých rohů se míčky vůbec nedostanou, a ve zbytku určit podíl aktivovaných pastí.
Minové pole
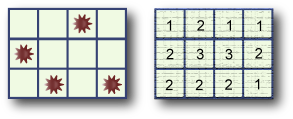 Zadání: Na minovém poli jsou rozmístěny miny. Nevíme přesně, kde miny jsou, ale u každého políčka víme, kolik je na něm a v jeho okolí min (celkem na devíti políčcích). Naším úkolem je zjistit, kolik min může být maximálně v prostřední řadě políček (počet řad je vždy lichý). Řešení [ #finals-c ]
Zadání: Na minovém poli jsou rozmístěny miny. Nevíme přesně, kde miny jsou, ale u každého políčka víme, kolik je na něm a v jeho okolí min (celkem na devíti políčcích). Naším úkolem je zjistit, kolik min může být maximálně v prostřední řadě políček (počet řad je vždy lichý). Řešení [ #finals-c ]
Řešení: Osobně bych vyzkoušel všechny možnosti a postupem od větví, které se můžou nejméně rozvětvit, bych se pokusil minimalizovat čas testování. Existuje ale i elegantnější řešení – počet min v prostřední řadě totiž přímo plyne z mapy čísel. Stačí si uvědomit, že počet min v každé devítici políček je určen číslem uprostřed tohoto čtverce (pro krajní šestice to určuje prostřední políčko u okraje). Takto můžeme zjistit počet min v každé trojici řad a tím pádem i v horních a dolních (N + 1) / 2 řadách. A když od součtu těchto řad (kde je prostřední řada dvakrát) odečteme celkový počet min získaný stejným způsobem, máme přesně počet min v prostřední řadě.
function mines($number) {
$cols = count($number);
$return = 0;
for ($i = ($cols % 3 ? 0 : 1); $i < $cols; $i += 3) {
$return += $number[$i];
}
return $return;
}
function minelayer($numbers) {
$rows = count($numbers);
$return = 0;
for ($j = ($rows + (($rows - 1) % 6 ? 1 : 3)) / 2; $j < $rows; $j += 3) {
$return += mines($numbers[$j]);
$return += mines($numbers[$rows - $j - 1]);
}
for ($j = ($rows % 3 ? 0 : 1); $j < $rows; $j += 3) {
$return -= mines($numbers[$j]);
}
return abs($return);
}Pokud je polovina počtu řádek dělitelná třemi, tak prostřední řádku nelze lehce započítat dvakrát, dá se ale naopak velmi snadno vynechat. Z tohoto důvodu se na konci funkce vrací absolutní hodnota rozdílu.
Stavitelé mostů
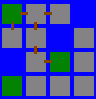 Zadání: Máme zadanou mapu, kde je na každém čtverečku les, voda nebo pole. Mezi čtverečky je voda. Naším cílem je propojit tyto ostrovy pomocí mostů, které z daného políčka můžou vést vždy jen na horní, dolní, levý nebo pravý ostrov. Mosty se staví ze dřeva nalezeného v lese a postavit most trvá člověku tolik hodin, jaká je vzdálenost od nejbližšího lesa k propojovanému ostrovu. Na mapě na začátku nejsou žádné mosty a začínáme v levém horním rohu, kde je vždy les. Naším úkolem je propojit všechny ostrovy za minimální počet člověko-hodin a vrátit tento počet. Řešení [ #finals-d ]
Zadání: Máme zadanou mapu, kde je na každém čtverečku les, voda nebo pole. Mezi čtverečky je voda. Naším cílem je propojit tyto ostrovy pomocí mostů, které z daného políčka můžou vést vždy jen na horní, dolní, levý nebo pravý ostrov. Mosty se staví ze dřeva nalezeného v lese a postavit most trvá člověku tolik hodin, jaká je vzdálenost od nejbližšího lesa k propojovanému ostrovu. Na mapě na začátku nejsou žádné mosty a začínáme v levém horním rohu, kde je vždy les. Naším úkolem je propojit všechny ostrovy za minimální počet člověko-hodin a vrátit tento počet. Řešení [ #finals-d ]
Řešení: Mapu budeme procházet do šířky a u každého políčka si poznamenáme, jak je daleko od nejbližšího lesa. Jakmile dorazíme do nějakého lesa, zapíšeme do něj nulu, ale nesmíme zapomenout připočítat cestu, kterou jsme museli urazit z předchozího lesa. Výsledkem je potom součet vzdáleností všech políček od nejbližšího lesa a napočítaných cest mezi lesy.
function bridges($map) {
$queue = array(array(0, 0, 0));
$return = 0;
$distances = array();
while ($queue) {
$val = min($queue);
unset($queue[array_search($val, $queue)]);
list($distance, $y, $x) = $val;
if (isset($map[$y]{$x}) && $map[$y]{$x} != '.' && (!isset($distances["$y:$x"]) || $distance < $distances["$y:$x"])) {
if ($map[$y]{$x} == 'T') {
$return += floor(($distance + 2) / 2) * ceil($distance / 2);
$distance = 0;
}
$distances["$y:$x"] = $distance;
$queue[] = array($distance+1, $y-1, $x);
$queue[] = array($distance+1, $y+1, $x);
$queue[] = array($distance+1, $y, $x-1);
$queue[] = array($distance+1, $y, $x+1);
}
}
return $return + array_sum($distances);
}V každém průchodu cyklem se hledá nejmenší prvek pomocí funkcí min a array_search, využívají se přitom pravidla pro porovnávání polí [ http://www.php.net/manual/en/language.operators.comparison.php ]. Nové ostrovy ke zkontrolování by se do pole $queue mohly zatřiďovat, což by trvalo jen O(log n) místo O(n). Algoritmus je ale dost rychlý i bez toho.
Pro započtení vzdálenosti mezi lesy se používá součet posloupnosti každého druhého čísla. Protože pokud to do lesa bylo např. 5 hodin, tak 5 přepíšeme na 0 (rozdíl 5), 4 na 1 (rozdíl 3) a 3 na 2 (rozdíl 1).
