
V dnešním díle si ukážeme příklad, který vyřešíme pomocí všech tří typů cyklů. Dále si ukážeme typ úlohy, pro kterou je vhodnější použití cyklu s podmínkou na začátku. A nezapomene na příklad se zadáním PINu do mobilu.
Součet N čísel
V prvním dnešním příkladu si ukážeme, že úlohu lze řešit všemi typy cyklů. Podobnou úlohu už jsme řešili. Zadání té aktuální by mohlo znít: vytvořte algoritmus pro součet N zadaných čísel, kdy nejprve zadáme kolik čísel budeme sčítat a následně tato čísla postupně načteme a provedeme jejich součet. Na vstupu od uživatele dostaneme nejprve počet čísel (N) a následně uživatel zadá N různých čísel, které budeme sčítat. Výsledkem algoritmu bude výpis tohoto součtu.
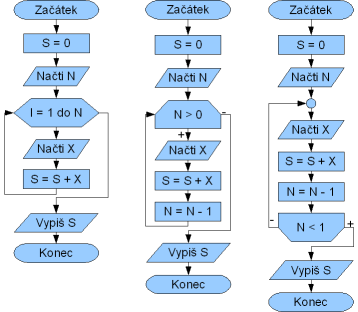
Řešení pomocí cyklu s daným počtem opakování se nabízí a stále je pro tento typ úloh nejvhodnější. Rozmezí cyklu bude od 1 do zadaného N. V těle se načítají čísla od uživatele (X) a provádí se jejich součet do S. Proměnnou S nesmíme zapomenout před vstupem do cyklu inicializovat na 0. Po jeho skončení máme v S výsledný součet, který vypíšeme. Vývojový diagram je vidět na obrázku v jeho levé části.
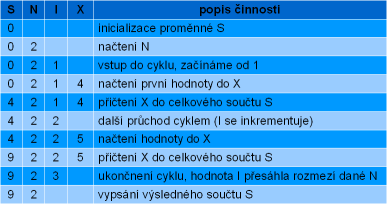
Použití cyklu s podmínkou na začátku nebo na konci není sice to nejlepší řešení, ale je možné. Základ bude stejný, jen potřebujeme počítat počet zadaných čísel, abychom jich opět zadali pouze N. V proměnné N máme celkový počet, takže můžeme jít podobnou cestou jako u cyklu s daným počtem opakování, tj. do další proměnné bychom si ukládali počet již zadaných čísel. Podmínka by kontrolovala, jestli počet načtených čísel se rovná N.
Vzhledem k tomu, že hodnotu proměnné N zadanou uživatelem již nikde nevyužíváme, tak ji můžeme „znehodnotit". Použijeme princip stříhání metru, kde se za každý den čekání odstřihne jeden dílek. My budeme za každé zadané číslo uživatelem snižovat hodnotu N o 1.
Vývojový diagram opět začíná inicializací S na 0 a zadáním hodnoty N. Následuje vstup do cyklu přes jeho podmínku. Tělo se opakuje, dokud je podmínka splněna, tj. dokud je co „stříhat". V našem případě dokud jsme nezadali všech N čísel, neboli dokud je hodnota v N větší než 0.
Tělo cyklu je téměř stejné. K zadávání a sčítání jsme přidali zmenšování hodnoty N o 1 (stříhání metru). Cyklus skončí ve chvíli, kdy hodnota N bude 0 (nebo menší) – již není co stříhat. Algoritmus bude funkční i v případě, že uživatel zadá do N nulové nebo záporné číslo.
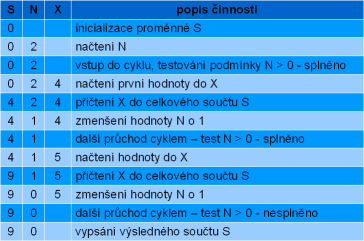
Řešení pomocí cyklu s podmínkou na konci je nejméně vhodné. Rozdíl proti řešení s podmínkou na začátku je hlavně v podmínce – cyklus pokračuje v případě, že není podmínka splněná (dělej, dokud není N menší než 1). Jinak je algoritmus v podstatě stejný. Problém tohoto řešení je v tom, že nebude dobře fungovat, pokud uživatel zadá N nulové nebo záporné. I v takovém případě se provede tělo cyklu, takže uživatel bude nucen zadat jedno číslo a výsledný součet tak nemusí být 0.
Vstup od uživatele (
Pohyb vozíku
Na této úloze si ukážeme, že je nutné zamyslet se nad výběrem cyklu a jeho podmínky. Máme vozík, který se pohybuje po koleji (má jeden stupeň volnosti). Na koncích koleje jsou senzory, které nám řeknou, že vozík dosáhl konce a dál nemůže. Naším úkolem je vytvořit algoritmus pro automatický pohyb po koleji v jednom směru. Úloha je velmi zjednodušená a půjde pouze o demonstraci vhodnosti volby typu cyklu a podmínky.
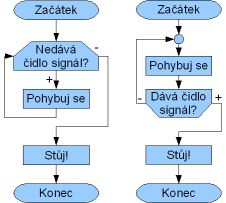
Úlohu vyřešíme oběma typy cyklů s podmínkou. Začneme tím vhodnějším, a to s podmínkou na začátku. Tělo tohoto cyklu se vykonává, dokud je podmínka splněná, takže se bude vykonávat (pohybovat vozíkem), než nám čidlo dá vědět, že jsme na konci. Jak vidíte, tak vývojový diagram je velice jednoduchý. Testujeme hodnotu z čidla a pokud ještě nejsme na konci, tak se pohybujeme. Ve chvíli, kdy senzor „zabere", tak zastavíme pohyb a ukončíme program.
Stejně jako v předchozím případě (se záporným číslem) je toto řešení odolné i na mezní případ, a to ten, že vozík stojí na senzoru. Na verzi s cyklem na konci si ukážeme slibované problémy.
Vývojový diagram je opět jednoduchý. Podmínka je samozřejmě opačná než v předchozím případě. Když jsme např. uprostřed kolejnice, tak i s tímto typem cyklu dosáhneme konce. V čem je tedy problém?
Problém je v krajním případě, tj. pokud vozík stojí na senzoru. V takovém případě by se s tímto typem cyklu dal vozík i tak do pohybu (nejprve se provádí tělo cyklu – pohyb). A pokud by čidlo dávalo stop signál pouze na té jedné pozici, tak by se již vozík nezastavil a vykolejil by. Drobná „chyba", která se nemusí za celou dobu používání projevit, může mít v případě jejího „objevení" fatální následky.
Na obrázku vidíte, že cykly jsou opět velmi podobné. Jediné, v čem se liší, je podmínka, kterou se řídí.
PIN
Poslední dnešní příklad je slibované zadávání PINu do mobilu. Tuto činnost dělá valná většina z vás několikrát do měsíce, takže je všeobecně známá. Máme tedy za úkol vytvořit algoritmus pro zadávání PINu do mobilu s tím, že je možné maximálně 3× po sobě zadat špatný PIN a pak se mobil zablokuje. V případě správného zadání PINu se mobil aktivuje.
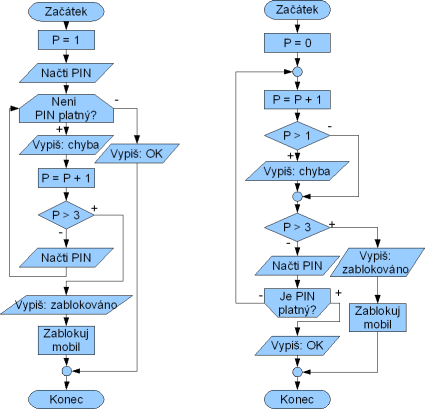
Na vstupu od uživatele tedy bude PIN, který následně otestujeme. Výsledkem algoritmu bude buď aktivní mobil, nebo zablokovaný mobil. Úlohu si vyřešíme opět pomocí obou typů cyklů s podmínkou, a to s úplným ošetřením vstupu od uživatele i možných chybových stavů (v rámci zadávání).
Začneme cyklem s podmínkou na začátku. Abychom měli co vyhodnocovat v podmínce, musíme PIN zadat před ní. Jde vlastně o první pokus, takže počáteční hodnotu počítadla pokusů (P) můžeme nastavit na 1. Po vyhodnocení jsou 2 možnosti: buď je PIN neplatný a cyklus pokračuje dále, nebo je PIN platný a je možné aktivovat mobil a skončit.
V případě, že PIN není platný (a taková musí být i podmínka), je o této skutečnosti nutno informovat uživatele. Vypíšeme, že PIN není platný a přejdeme na další pokus zadávání PINu. Ještě před zadáním si musíme ověřit, že se nejedná o čtvrtý a další pokus, protože v takovém případě je nutné zadávání ukončit a zablokovat mobil. Na obrázku vývojového diagramu vidíte jedno z možných uspořádání. Mohli bychom bloky uspořádat i jinak, např. počítání pokusů dát až za zadání PINu, ale v takovém případě by podmínka musela být P > 2. Ve výsledku dostanem tu samou funkčnost.
To je v podstatě vše. Ve výsledném algoritmu je jedna nová věc, cyklus má vlastně dvě možnosti ukončení. Jedna možnost je standardní, a to při nesplnění podmínky cyklu. Druhá možnost ukončení je od vložené podmínky, při jejím splnění se cyklus také ukončí. Toto je poměrně běžná praxe, kdy cyklus končí za nějakých (optimálních) podmínek a přes podmínky se vkládá ukončení cyklu například při nějak chybě nebo „neočekávané" situaci. A také se takového ukončení využívá u „nekonečných" cyklů, tj. cyklů, které by bez další dodatečné možnosti ukončení běžely neustále.
Řešení pomocí cyklu s podmínkou na konci je pro tuto úlohu lepší varianta, ale když porovnáte vývojové diagramy, tak zjistíte, že jsou v podstatě stejné. Velký rozdíl je, a to už jsme vyzdvihli v některém z minulých dílů, že se PIN zadává na jednom místě. Naproti tomu musíme rozlišit v těle cyklu, kdy se jedná o první zadávání a kdy o následné, abychom případně mohli vypsat hlášení uživateli, že PIN není správně.
Stejně jako v řešení s podmínkou na začátku lze bloky v těle cyklu poskládat více způsoby. Důležité je před zadáváním zjistit, jestli se má vypsat hlášení nebo jestli už by se nejednalo o 4. pokus (P > 3). Pokud bychom umístili počítání za zadávání PINu, pak bychom opět museli upravit obě podmínky (na P > 0 a P > 2).
Vývojový diagram také obsahuje 2 možnosti ukončení (stejnou možnost lze využít i v cyklu s daným počtem opakování). Výsledný vývojový diagram si můžete prohlédnout na obrázku a případně zkontrolovat jeho funkci tabulkami hodnot pro různé možnosti (vlastně jsou čtyři: správně zadaný PIN na první, druhou a na třetí možnost a 3× nesprávně zadný PIN).
Tím dnešní díl zakončíme, příště se podíváme na složitější příklady, kde využijeme nejenom více cyklů, ale hlavně jejich kombinace.
