
Psaní článku pomocí LaTeXu ocení především studenti matematických, fyzikálních a přidružených oborů, kde je potřeba sepisovat práce s velkým množstvím matematických zápisů - např. rovnic. Dnes si ukážeme, jak do našich textů snadno vkládat matematické symboly či vzorce, a vytvoříme jako příklad menší výukový materiál pro funkce více proměnných.
Poznámka autora: Prvně menší omluva, minule jsme si slíbili článek navazující na psaní dokumentů. Rozhodl jsem se však mírně přeorganizovat strukturu tohoto seriálu, proto je tématem třetího článku matematika.
Pro sázení matematických symbolů využíváme několika způsobů, postupně si představíme, jak se pohybovat v matematických zápisech, navíc v závěru naleznete několik doporučení a odkazy na různé stránky.
V tomto díle si budeme spíše ukazovat přístup k matematickým zápisům než se učit samotné zápisy. Matematických symbolů je totiž nezměrné množství, vyložit je zde by vůbec nebylo efektivní, v případě psaní matematických součástí vašich dokumentů se budete muset spoléhat sami na sebe. Dost nápomocný je např. odkaz na anglickou Wikipedii, poté zmíněná možnost zobrazení stavby, v zásadě ale bude potřeba často využívat Google.
Obecné zápisy
Speciální znaky a rovnice v textu
První věcí, kterou můžeme požadovat, je, abychom měli nějaký matematický symbol v řádce, např. situace na následujícím obrázku by se v LaTeXu zapsala jako
Nechť je dána funkce $f(\xi): \Omega\to\mathbb{R}$, kdy $\Omega$ je otevřená množina, tj. $\Omega\in\mathcal{G}$.
Vidíme, že pokud se chceme zabývat nějakým speciálním zápisem v řádce, musíme provést oddělení klasického textu od toho, který se má zpracovávat speciálním způsobem. Toto oddělení děláme pomocí dolaru $ (pro ty z vás, kteří netuší, jak efektivně psát tento znak, mně se při psaní všemi deseti osvědčila zkratka (levý alt)+(levý ctrl)+ů na české klávesnici - věřím, že se toho dá využít i jinde, např. v PHP). Obecně tedy budeme seznávat pravidlo, budeme-li chtít přidat nějaký zápis do prostého textu, které říká:
"Chci-li zadat do prostého textu speciální znak či posloupnost takových znaků (např. rovnici), oddělím tuto mnou psanou část symboly dolaru."
Později si všimneme na příkladu sumy, jak se budou chovat indexy v tomto prostředí.
Speciální znaky a rovnice na vlastní řádce
Příkladem takového zápisu nechť jest zápis na následujícím obrázku.
Docílit takového zápisu můžeme pomocí několika metod a předem poznamenejme, že pro obyčejného pisálka není vůbec rozhodující, kterou z variant použije.
"Dvojdolar"
Pokud chceme psát na speciální řádek, můžeme matematický zápis oddělit pomocí dvojdolaru $$, tj.
Tohle je prostý text, dále bude rovnice $$ x - y = z + 4\Omega. $$
Prostředí equation
Další možností je napsat kód
Tohle je prostý text, dále bude rovnice
\begin{equation}
x - y = z + 4\Omega.
\end{equation}
Narozdíl od zápisu pomocí dvojdolaru je však nyní rovnice očíslovaná vpravo.
Prostředí align
V prostředí align můžeme mít dvojího zápisu.
Tohle je prostý text, dále bude rovnice
\begin{align}
x - y = z + 4\Omega.
\end{align}
Místo align můžeme také psát align*, čímž způsobíme, že rovnice se nebudou číslovat. O číslování rovnic si povíme hned v další kapitolce.
Odkazy na číslované prvky v prostředí equation či align
Občas se potřebujeme při psaní textu odkazovat na nějakou rovnici, např. rovnice v následujícím obrázku nechceme neustále psát znovu a znovu, jelikož jsou příliš dlouhé, odkazujeme se na ně proto jako na rovnice (3) a (4).
Efektu na obrázku dosáhneme pomocí kódu
Besselovou rovnicí $\mu$. řádu rozumíme obyčejnou diferenciální rovnici ve tvaru
\begin{align}
\label{besselova_rovnice} z^2\frac{d^2f(z)}{dz^2}(z) + z\frac{df}{dz}(z) + (z^2 + \mu^2)f(z) = 0.
\end{align}
Besselovou funkcí prvního řádu $J_\mu(z)$ rozumíme funkci
\begin{align}
\label{besselova_J} J_\mu(z) = \left(\frac{z}{2}\right)^\mu\sum_{k=0}^\infty\frac{(-1)^k}{k!\Gamma(\mu+k+1)}\left(\frac{z}{2}\right)^{2k}.
\end{align}
Dá se snadno ukázat, že funkce \eqref{besselova_J} je řešením rovnice \eqref{besselova_rovnice}.
Vidíme, že tedy používáme spojení \label{ název } <-> \eqref{ název }. Pokud si článek čtete poprvé, zřejmě ještě netušíte, co přesně znamenají jednotlivé zápisy jako \frac{}{} apod., nebojte se však, vše si vysvětlíme níže. Pokud se po skončení čtení tohoto článku podíváte zpětně na tuto část, měli byste již plně rozumět tomu, oč jde.
Poznámka: Výhoda TeXMakeru, který jsme si doporučovali v úvodním článku, je jeho uživatelská přátelskost (je velice user-friendly). Pokud kdekoliv v textu použijete \label{...} a poté začnete psát \eqref{}, automaticky vám již nabízí možnosti rovnic označených pomocí \label{}.
Finálně si tedy můžeme říci pravidlo pro psaní speciálních znaků a rovnic do speciálního bloku:
"Chci-li psát speciální znaky či rovnice do speciálního bloku, použiji buďto dvojdolar $$, či prostředí equation či align(*). Navíc můžu rovnice očíslovat a poté se na ně odkazovat pomocí spojení \label{název} <-> \eqref{název}."
Základní matematické zápisy
Coby základ bychom se měli naučit základní matematické zápisy algebraických výrazů, indexování apod. Jedná se tedy v zásadě o psaní algebraických operátorů (krát apod.), odtud i zlomky, mocniny atd.
Jako první poznamenejme, že veškeré matematické zápisy zapisujeme do prostředí uzpůsobeného pro psaní matematiky (to jsou např. prostředí equation, align nebo psaní mezi dolary v textu, jak jsme si vysvětlili výše).
Seznam znaků pro běžné psaní včetně příkladů je možné najít v následující tabulce. Do tabulky zahrnujeme také indexování (spodní, horní index), zlomky a základní věci, které jsou využívány velmi často.
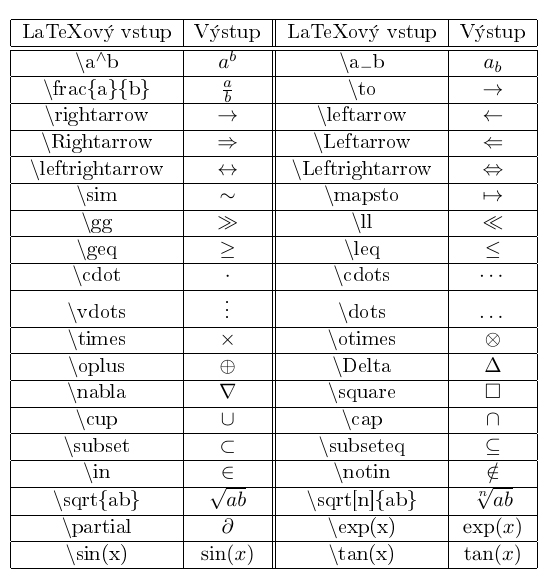
Je samozřejmě sporné, zda se zde vyskytují veškeré často používané znaky. Faktickou krásou TeXMakeru, který někteří využíváme, je, že pokud si necháme zobrazovat stavbu, poté si můžeme většinu znaků naklikat (nebojte se, stačí si znak nakliknout jednou a ve zdrojovém kódu se samozřejmě zobrazí coby \heslo_znaku) - zobrazení stavby nastavíme pomocí Pohled -> Stavba. Navíc můžeme spoustu inspirace najít na anglické Wikipedii - LaTeXové příklady. Pokud byste ani tak svůj znak nenašli, můžete jej myškou nakreslit do políčka na Detexify a dostanete nabídky, jak by mohl váš znak vypadat.
Dalším poznatkem jsou hodnoty vkládané do argumentů. Podívejme se na příklad horního indexu - mocniny. Chceme-li umocnit číslo 2 na hodnotu (a + b), zřejmě bychom intuitivně napsali
2^(a+b)
To by nám ovšem nedalo správný výstup. V horním indexu je vždy pouze první znak - v našem případě závorka. Abychom umocnili 2 na celou závorku, využijeme místo kulatých závorek složené - všimněme si, že složené závorky prostupují celým zápisem - tedy 2^{a+b} již dá správný výsledek.
Závorky
Závorky jsou velmi často využívaná věc, ať už máme na mysli (), [], {} atd. Časem se ale každý setká např. s umocňováním zlomků, které by podle předešlé tabulky vypadalo jako ( \frac{a}{b} )^n. Zkuste si schválně, jaký dostanete výsledek - závorky nebudou velké přes celý zlomek, ale budou mít standardní velikost na jeden řádek. Proto využíváme pro větší závorky \left a \right. Ve finále bude správný kód vypadat takto:
\left( \frac{a}{b} \right)^n
Upozornění: V dokumentu musíme použít stejným počtem left i right. Pokud bychom měli dvakrát \left( a pouze jednou \right), potom se nám dokument nesloží a překladač vyhodí chybu.
Řecká písmena
U řeckých písmen je zápis jednoduchý. Napíšeme prostě \recke_pismeno, např. \alpha, \beta, \gamma, \psi, \phi atd. Velká řecká písmena píšeme s prvním písmenem velkým - \Psi, \Gamma, \Omega.
Druhy písma v matematickém prostředí
V matematice se často setkáváme se zdvojenými písmeny - např. reálná čísla můžeme značit tučným R nebo právě zdvojením. Mimo zdvojení využíváme často také dalších typů písem. Následující tabulka ukazuje druhy písem s příklady využití.
Speciální symboly
V případě psaní symbolů se setkáváme se psaním \znak, to samo o sobě znamená, že znak \ je pro nás značením příkazu, pokud jej však chceme v dokumentu použít, musíme jej nahradit sekvencí $\backslash$. Seznam speciálních znaků můžete opět najít pomocí internetového vyhledávače či na odkazované Wikipedii. Zde uvedu seznam těch, které využívám s největší četností já.
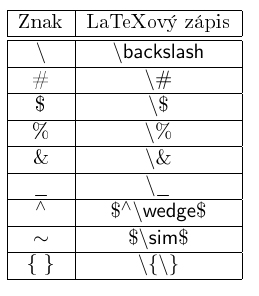
Poznámka: U symbolů ^ a ~ využíváme matematického prostředí. Není to nutné, ale osobně mi to přijde jako nejsnazší cesta. Uvádí se také možnost zapsat ^ pomocí \^{}, to ovšem mně nefunguje, tak zde raději uvádím svou osvědčenou metodu, jak symboly zapisovat.
Velké operátory
Velkými operátory máme na mysli operátory typu: integrál, suma... zkrátka takové operátory, u kterých běžně zapisujeme indexy a výraz za operátorem je daný obecným zápisem. V tabulce máme opět přehled nejčastěji používaných operátorů.
Ze zápisu jazyka vidíme, že indexujeme tradičně pomocí znaků ^ a _. Sloupec s názvem Limits udává, jak vypadá daný operátor, pokud za něj dodáme \limits. Ukažme si to na příkladě integrálu: Ve sloupci Výstup v prvním řádku máme \int_a^b, kdežto ve sloupci Limits téhož řádku máme \int\limits_a^b.
Matice
Ať chceme nebo ne, pokud musíme pracovat s maticemi, je vhodné umět je zapisovat pomocí LaTeXu, neboť je zbytečné jen kvůli maticím odcházet od psaní tímto stylem.
Matice je anglicky matrix a prostředí, které budeme nyní používat, bude spojeno právě s tímto slovíčkem. Jsme samozřejmě stále v matematickém prostředí a do něj můžeme vložit následující kód:
\begin{matrix}
A & B & C \\
D & E & F
\end{matrix}
Pokud si necháte takový kód přeložit v TeXMakeru, dostanete jako výstup obdélníkové schéma čísel. Jednotlivé sloupce v řádku oddělujeme pomocí znaku & a konec řádky (mimo tu poslední) provádíme pomocí \\. Všimněme si ovšem, že zde není matice zapsaná pomocí závorek (okolo obdélníku čísel nejsou žádné závorky). Pokud bychom chtěli mít závorky kulaté, použijeme do příkladu místo matrix pmatrix. Pokud bychom chtěli rovné (např. při zápisu determinantu), poté vmatrix.
NewCommand
Na závěr si povězme, jak používat definování vlastních příkazů pomocí \newcommand, to je totiž velice oblíbená praktika např. při vytváření vlastních operátorů. \newcommand má jak hodnotu (a dokonce dvě hodnoty), tak nějaké další parametry, to znamená, že celá struktura příkazu je
\newcommand{ hodnota_nová }[ parametry ]{ hodnota_stará }
Parametr využívat můžeme a nemusíme. Příkaz \newcommand píšeme před začátek samotného textu dokumentu, tedy ještě před \begin{document}. Nejprve se podívejme na snazší příklad - kdy jej využívat nebudeme.
\newcommand{\Rot}{\nabla\times}
Kdekoliv v textu poté můžeme používat příkaz \Rot a v místě jeho použití se bude brát pro překlad LaTeXového kódu \nabla\times (co dané prvky znamenají, není v tuto chvíli důležité, jste-li zvědaví, podívejte se na tabulku níže v článku).
Situace s parametrem bude o něco složitější, i když ne o moc. Víme, že někdy můžeme používat \prikaz a někdy zase \prikaz{}. Např. u zlomku máme \frac{čitatel}{jmenovatel}. Parametr je tedy počet hodnot, které chceme do nového příkazu zadávat. Nejsnazší pochopení toho bude na příkladě:
\newcommand{\str}[2]{\langle #1 | \hat{#2} | #1 \rangle}
...
\str{a}{H}
Pro ty z vás, kdo tuší, jedná se o střední hodnotu Hamiltoniánu ve stavu a v kvantové mechanice. Opět není důležité, jak samotný příkaz vypadá, ale vidíme, že první z vložených hodnot se umístí na pozici #1 a druhá na pozici #2.
NewCommand tedy využváme v situacích, kdy musíme neustále opakovat stejný kód dokola, můžeme jej připodobnit k podobě funkcí v programování - dodáváme vstupní parametry a získáváme jeden výstup.
Příklad na konec a úkol na procvičení
Nyní si ukážeme příklad, jak zavést nový operátor, který nazveme intoi (integral od 0 do nekonec - infty). Vytvoříme jej dvěma způsoby - s argumentem a bez argumentu. Navíc požadujeme, aby meze integrálu byly přesně pod značkou integrálu (využijeme \limits).
První způsob je jednoduchý, využijeme na začátku popisovanou metodu vytvoření nového příkazu pomocí \newcommand:
\newcommand{\intoi}{\int\limits_0^\infty}.
To nám stačí, poté můžeme v textu napsat \intoi a vypíše se příslušný operátor integrálu na kladných číslech. Vyzkoušejte si sami tento kód. Druhým způsobem je
\newcommand{\intoi}[1]{\int\limits_0^\infty #1 dx}.
Opět si vyzkoušejte a zjistíte, co daný výraz dělá.
A nyní úkol na procvičení. Zkuste pomocí newcommand zavést následující operátory:
- integrál přes všechna reálná čísla (dole v indexu R),
- mocninnou řadu s dosazovaným argumentem z,
- operátory: gradient, divergence, rotace (příslušný znak je \nabla).
Dále zapište matematicky číslovanou
- binomickou větu,
- definici multiindexu,
- definici limity posloupnosti a limity funkce,
- definici derivace funkce více proměnných ve směru vektoru v.
Napište potom krátký text a odkazujte se na příslušné číslované věty pomocí \eqref. Úplně na závěr je zde obrázek, který byste měli být schopni přepsat do LaTeXu, přestože nemusíte rozumět, o čem pojednává.
 TIP: Přetáhni ikonu na hlavní panel pro připnutí webu
TIP: Přetáhni ikonu na hlavní panel pro připnutí webu


 Ukázka prostředí pro psaní rovnic. Na horním obrázku vidíme číslovanou rovnici a na spodním nečíslovanou.
Ukázka prostředí pro psaní rovnic. Na horním obrázku vidíme číslovanou rovnici a na spodním nečíslovanou.







