Dobrý den, co je prosím špatně na tomto kódu (asi je chyba v poslední části # Perpendicular line), že není zelená přímka kolmá k oranžové tečně? Děkuji.
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.patches as patches
fig, ax = plt.subplots(figsize=(10,3))
x_start = -2
x_end = 32
x = np.linspace(x_start, x_end, 1000)
def f(x):
a = 1
mu1 = 5
mu2 = 25
sigma = 2.5
y1 = a*np.exp(-(x-mu1)**2/(2*sigma**2))
y2 = a*np.exp(-(x-mu2)**2/(2*sigma**2))
return y1+y2
y=f(x)
def deriv(f,x):
h = 0.000000001 # step-size
return (f(x+h) - f(x))/h # definition of derivative
def tangent_line(f, x_0, a, b):
x = np.linspace(a, b, 1000)
y = f(x)
y_0 = f(x_0)
y_tan = deriv(f,x_0) * (x - x_0) + y_0
P = (x_0, y_0)
return y_tan
plt.plot(x, y)
plt.xlim(15, x_end)
plt.ylim(-0.05, 1.8)
# Chose a point and plot a tangent
C = 270
l = 30
y_tan = tangent_line(f,x[-C],-2,32)
cor = 0.02
# Tangent
plt.plot(x[-C-l:-C+l], y_tan[-C-l:-C+l])
# Perpendicular line
P1 = (x[-C-l:-C+l][0], y_tan[-C-l:-C+l][0])
ax.scatter(x[-C-l:-C+l][0], y_tan[-C-l:-C+l][0])
b = (x[-C], y[-C])
ax.scatter(x[-C], y[-C])
u = [b[0] - P1[0], b[1] - P1[0]]
plt.scatter(b[0] - P1[0], b[1] - P1[1])
u_per = (u[1], u[0])
shorten = 0.45
P_per = (b[0] + shorten * u_per[0], b[1] + shorten * u_per[1])
plt.scatter(b[0] + shorten * u_per[0], b[1] + shorten * u_per[1])
plt.plot([b[0], P_per[0]], [b[1], P_per[1]])
plt.show() TIP: Přetáhni ikonu na hlavní panel pro připnutí webu
TIP: Přetáhni ikonu na hlavní panel pro připnutí webu


 Newbie
Newbie


 Nahlásit jako SPAM
Nahlásit jako SPAM IP: 2a00:1028:9197:cbb6:d0ad:79c:9a72:b8a2...–
IP: 2a00:1028:9197:cbb6:d0ad:79c:9a72:b8a2...–

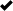 Nejlepší odpověď
Nejlepší odpověď
 Zjistit počet nových příspěvků
Zjistit počet nových příspěvků

































