Stereometrie-odchylka přímky od roviny – Matematika – Fórum – Programujte.com

 Mohl by mi někdo ochotný napsat vzorečky a postup, jak tento příklad počítal? Já jsem to zkoušela, ale vůbec mi to nevyšlo :(
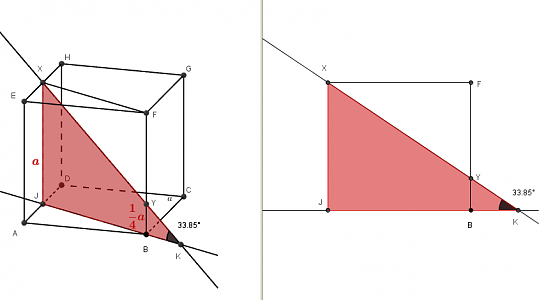
Je dána krychle ABCDEFGH. Určete ochylku přímky p = XY od roviny $\varrho = ABC, kde X je střed hrany EH, bod Y je bod hrany BF, BY : YF = 1 : 3.

#1 Tabb
Máš dvě možnosti jak to spočítat.(pro jednoduchost položíme a=1-to lze, protože počítáme úhel přes nějakou geometrickou funkci a to je vždy nějaký poměr, kde by se délka vykrátila)

1. Z obrázku (přes funkci tangens)

   JB=sqrt(1+1/4)=sqrt(5)/2,     JX=1,   BY=1/4

   Z podobnosti trojúhelníků JKX a BKY se dá lehce spočítat velikost úsečky BK (označme ji x)

  JX/BY=(JB+x)/x   a tedy 1/(1/4)=(sqrt(5)/2+x)/x       .....   x=sqrt(5)/6

  a pak tg(fi)=1/(sqrt(5)/2+sqrt(5)/6)=3/(2sqrt(5))  a fi=33.85451 stupně.

nebo

2. Jako úhel dvou přímek přes jejich směrové vektory (označme je s1 a s2)

    Vyjádříš parametrické rovnice obou přímek

    přímka 1   x=0+t, y=1/2-1/2*t, z=1-3/4*t  a tedy směrový vektor s1=(1,-1/2,-3,4)=(s11,s12,s13)  (s11=1,první   souřadnice vektoru s1 atd)

    přímka 2   x=0+t, y=1/2-1/2*t, z=0+0*t a tedy směrový vektor s1=(1,-1/2,0)=(s21,s22,s23)

    cos(fi)=s1*s2/(velikost9s1)*velikost(s2))=(s11*s21+s12*s22+s13*s23)/sqrt((s11^2+s12^2+s13^2)(s21^2+s22^2+s23^2))

    cos(fi)=(1+1/4+0)/sqrt((1+1/4+9/16)(1+1/4+0)    a pak fi=33.85451 stupně.

#1 Tabb
Máš dvě možnosti jak to spočítat.(pro jednoduchost položíme a=1-to lze, protože počítáme úhel přes nějakou geometrickou funkci a to je vždy nějaký poměr, kde by se délka vykrátila)

1. Z obrázku (přes funkci tangens)

   JB=sqrt(1+1/4)=sqrt(5)/2,     JX=1,   BY=1/4

   Z podobnosti trojúhelníků JKX a BKY se dá lehce spočítat velikost úsečky BK (označme ji x)

  JX/BY=(JB+x)/x   a tedy 1/(1/4)=(sqrt(5)/2+x)/x       .....   x=sqrt(5)/6

  a pak tg(fi)=1/(sqrt(5)/2+sqrt(5)/6)=3/(2sqrt(5))  a fi=33.85451 stupně.

nebo

2. Jako úhel dvou přímek přes jejich směrové vektory (označme je s1 a s2)

    Vyjádříš parametrické rovnice obou přímek

    přímka 1   x=0+t, y=1/2-1/2*t, z=1-3/4*t  a tedy směrový vektor s1=(1,-1/2,-3,4)=(s11,s12,s13)  (s11=1,první   souřadnice vektoru s1 atd)

    přímka 2   x=0+t, y=1/2-1/2*t, z=0+0*t a tedy směrový vektor s1=(1,-1/2,0)=(s21,s22,s23)

    cos(fi)=s1*s2/(velikost9s1)*velikost(s2))=(s11*s21+s12*s22+s13*s23)/sqrt((s11^2+s12^2+s13^2)(s21^2+s22^2+s23^2))

    cos(fi)=(1+1/4+0)/sqrt((1+1/4+9/16)(1+1/4+0))    a pak fi=33.85451 stupně.