
Poslední sada úloh letošního Google Code Jam byla zadaná ve finále. Některé úlohy jsou již obtížnější, ale jiné se stále soustředí spíše na rychlé vymyšlení jednoduchého algoritmu. Na stránkách soutěže se také objevil oficiální klíč k řešení všech dosud zveřejněných soutěžních úloh, kde lze najít podrobnější vysvětlení řešení problémů.
Džus
Zadání: Na párty jsme pozvali daný počet lidí. Každý z těchto lidí má rád džus namíchaný z přísad A, B a C. Problém je, že každému vyhovuje jiné množství těchto přísad. Naším úkolem je stanovit takové množství přísad, abychom uspokojili co nejvíc lidí. U každého člověka máme zadáno, kolik které přísady minimálně chce, aby mu džus chutnal (maximální součet přísad je stanoven jako číslo 10 000). Řešení
Řešení: U dvou přísad by se dalo postupovat tak, že bychom si do pole $plusminus u každého člověka poznamenali, od jakého do jakého množství jedné přísady mu džus bude chutnat. V tomto poli bychom pak hledali maximální hodnotu. Pro tři přísady stačí vyzkoušet sestavit toto pole pro všechny možné hodnoty třetí přísady.
function juices($people) {
$return = 0;
sort($people);
foreach (array_reverse($people, true) as $key => $val) {
list($a, $b, $c) = $val;
$plusminus = array();
foreach ($people as $val2) {
list($a2, $b2, $c2) = $val2;
if ($a + $b2 + $c2 <= 10000) {
$plusminus[$b2]++;
$plusminus[10001 - $a - $c2] -= 1;
}
}
ksort($plusminus);
$value = 0;
foreach ($plusminus as $val) {
$value += $val;
$return = max($return, $value);
}
unset($people[$key]);
}
return $return;
}Pro dekrementaci pole $plusminus se nepoužívá operátor --, ale konstrukce -= 1. Důvodem je, že hodnotu null operátor -- nesníží.
Pingpongové balónky
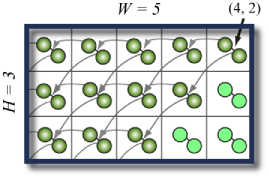 Zadání: Ve veliké místnosti zadaných rozměrů jsou na všech políčcích totožné pasti na myši. Každá past je nabita dvěma balónky, které se při aktivaci vystřelí na relativně zadané políčko a aktivují past, která na cílovém políčku leží. Naším úkolem je zjistit, kolik pastí se celkem aktivuje, pokud jako první aktivujeme past na určeném políčku. Řešení
Zadání: Ve veliké místnosti zadaných rozměrů jsou na všech políčcích totožné pasti na myši. Každá past je nabita dvěma balónky, které se při aktivaci vystřelí na relativně zadané políčko a aktivují past, která na cílovém políčku leží. Naším úkolem je zjistit, kolik pastí se celkem aktivuje, pokud jako první aktivujeme past na určeném políčku. Řešení
Řešení: Funkce začne na startovním políčku a ověří, jestli balónek ještě nevypadl z místnosti a jestli jsme dané políčko už nenavštívili. Pokud ne, tak nejprve aktivuje jeden balónek a potom druhý.
function pingpong($size, $ball1, $ball2, $x, $y, &$hits = array()) {
if ($x >= 0 && $x < $size[0] && $y >= 0 && $y < $size[1] && !isset($hits["$x:$y"])) {
$hits["$x:$y"] = true;
pingpong($size, $ball1, $ball2, $x + $ball1[0], $y + $ball1[1], $hits);
pingpong($size, $ball1, $ball2, $x + $ball2[0], $y + $ball2[1], $hits);
}
return count($hits);
}Pro vyřešení velkého vstupu by bylo potřeba zjistit, do jakých rohů se míčky vůbec nedostanou, a ve zbytku určit podíl aktivovaných pastí.
Minové pole
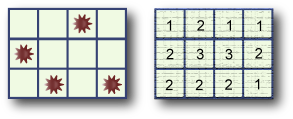 Zadání: Na minovém poli jsou rozmístěny miny. Nevíme přesně, kde miny jsou, ale u každého políčka víme, kolik je na něm a v jeho okolí min (celkem na devíti políčcích). Naším úkolem je zjistit, kolik min může být maximálně v prostřední řadě políček (počet řad je vždy lichý). Řešení
Zadání: Na minovém poli jsou rozmístěny miny. Nevíme přesně, kde miny jsou, ale u každého políčka víme, kolik je na něm a v jeho okolí min (celkem na devíti políčcích). Naším úkolem je zjistit, kolik min může být maximálně v prostřední řadě políček (počet řad je vždy lichý). Řešení
Řešení: Osobně bych vyzkoušel všechny možnosti a postupem od větví, které se můžou nejméně rozvětvit, bych se pokusil minimalizovat čas testování. Existuje ale i elegantnější řešení – počet min v prostřední řadě totiž přímo plyne z mapy čísel. Stačí si uvědomit, že počet min v každé devítici políček je určen číslem uprostřed tohoto čtverce (pro krajní šestice to určuje prostřední políčko u okraje). Takto můžeme zjistit počet min v každé trojici řad a tím pádem i v horních a dolních (N + 1) / 2 řadách. A když od součtu těchto řad (kde je prostřední řada dvakrát) odečteme celkový počet min získaný stejným způsobem, máme přesně počet min v prostřední řadě.
function mines($number) {
$cols = count($number);
$return = 0;
for ($i = ($cols % 3 ? 0 : 1); $i < $cols; $i += 3) {
$return += $number[$i];
}
return $return;
}
function minelayer($numbers) {
$rows = count($numbers);
$return = 0;
for ($j = ($rows + (($rows - 1) % 6 ? 1 : 3)) / 2; $j < $rows; $j += 3) {
$return += mines($numbers[$j]);
$return += mines($numbers[$rows - $j - 1]);
}
for ($j = ($rows % 3 ? 0 : 1); $j < $rows; $j += 3) {
$return -= mines($numbers[$j]);
}
return abs($return);
}Pokud je polovina počtu řádek dělitelná třemi, tak prostřední řádku nelze lehce započítat dvakrát, dá se ale naopak velmi snadno vynechat. Z tohoto důvodu se na konci funkce vrací absolutní hodnota rozdílu.
Stavitelé mostů
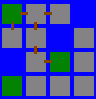 Zadání: Máme zadanou mapu, kde je na každém čtverečku les, voda nebo pole. Mezi čtverečky je voda. Naším cílem je propojit tyto ostrovy pomocí mostů, které z daného políčka můžou vést vždy jen na horní, dolní, levý nebo pravý ostrov. Mosty se staví ze dřeva nalezeného v lese a postavit most trvá člověku tolik hodin, jaká je vzdálenost od nejbližšího lesa k propojovanému ostrovu. Na mapě na začátku nejsou žádné mosty a začínáme v levém horním rohu, kde je vždy les. Naším úkolem je propojit všechny ostrovy za minimální počet člověko-hodin a vrátit tento počet. Řešení
Zadání: Máme zadanou mapu, kde je na každém čtverečku les, voda nebo pole. Mezi čtverečky je voda. Naším cílem je propojit tyto ostrovy pomocí mostů, které z daného políčka můžou vést vždy jen na horní, dolní, levý nebo pravý ostrov. Mosty se staví ze dřeva nalezeného v lese a postavit most trvá člověku tolik hodin, jaká je vzdálenost od nejbližšího lesa k propojovanému ostrovu. Na mapě na začátku nejsou žádné mosty a začínáme v levém horním rohu, kde je vždy les. Naším úkolem je propojit všechny ostrovy za minimální počet člověko-hodin a vrátit tento počet. Řešení
Řešení: Mapu budeme procházet do šířky a u každého políčka si poznamenáme, jak je daleko od nejbližšího lesa. Jakmile dorazíme do nějakého lesa, zapíšeme do něj nulu, ale nesmíme zapomenout připočítat cestu, kterou jsme museli urazit z předchozího lesa. Výsledkem je potom součet vzdáleností všech políček od nejbližšího lesa a napočítaných cest mezi lesy.
function bridges($map) {
$queue = array(array(0, 0, 0));
$return = 0;
$distances = array();
while ($queue) {
$val = min($queue);
unset($queue[array_search($val, $queue)]);
list($distance, $y, $x) = $val;
if (isset($map[$y]{$x}) && $map[$y]{$x} != '.' && (!isset($distances["$y:$x"]) || $distance < $distances["$y:$x"])) {
if ($map[$y]{$x} == 'T') {
$return += floor(($distance + 2) / 2) * ceil($distance / 2);
$distance = 0;
}
$distances["$y:$x"] = $distance;
$queue[] = array($distance+1, $y-1, $x);
$queue[] = array($distance+1, $y+1, $x);
$queue[] = array($distance+1, $y, $x-1);
$queue[] = array($distance+1, $y, $x+1);
}
}
return $return + array_sum($distances);
}V každém průchodu cyklem se hledá nejmenší prvek pomocí funkcí min a array_search, využívají se přitom pravidla pro porovnávání polí. Nové ostrovy ke zkontrolování by se do pole $queue mohly zatřiďovat, což by trvalo jen O(log n) místo O(n). Algoritmus je ale dost rychlý i bez toho.
Pro započtení vzdálenosti mezi lesy se používá součet posloupnosti každého druhého čísla. Protože pokud to do lesa bylo např. 5 hodin, tak 5 přepíšeme na 0 (rozdíl 5), 4 na 1 (rozdíl 3) a 3 na 2 (rozdíl 1).
 TIP: Přetáhni ikonu na hlavní panel pro připnutí webu
TIP: Přetáhni ikonu na hlavní panel pro připnutí webu






