
V tomto díle kurzu o fyzice se chci věnovat tomu, co by člověk měl znát, než se začne fyzikou jako takovou zabývat. V článku najdete povídání o fyzikálních veličinách a jednotkách, něco o matematickém aparátu, kterým byste měli disponovat pro zvládnutí kurzu, a poté nějaké matematické příklady, abyste si ověřili, zda to zvládnete.
Asi každý mi potvrdí, že pokud začnu rovnou s odvozováním vzorců, tak to nikomu moc nedá, každý totiž musí už přece něco znát do začátku. V tomto speciálním dílu se budu zabývat tím, co by měl člověk znát před samotným začátkem ve středoškolské látce předmětu fyzika.
Takže, jak začít? V úvodním článku jsme se přibližně dozvěděli, čím se fyzika zabývá a proč je užitečná, v tak krátkém příspěvku jsem ovšem nemohl popsat vše, to je nemožné. Nyní tedy začneme s opravdovým úvodem do fyziky.
Jak fyzika popisuje svět?
Už víme, že fyzika je věda, která se snaží popsat vesmír a principy, dle kterých se řídí. Jak to ale věda dokáže? Fyzika je velice úzce spjatá s matematikou, můžeme říci, že „polovina“ fyziky je matematika.
Matematikou popisujeme svět okolo sebe - křivku, po které se pohybuje padající míč, nebo velikost náboje. Z matematiky používáme funkce, konkrétně bychom mohli říci funkce jedné či více reálných proměnných. Uveďme si pro lepší pochopení příklad:
V matematice jsme zvyklí používat proměnné x a y, použijeme je tedy i zde. Představme si funkci, která vypadá takto:
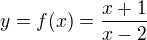
Tato funkce je zadána funkčním předpisem a vyskytují se v ní dvě reálné proměnné. Proměnná y je však závislou proměnnou, což znamená, že ve funkci je pouze jedna nezávislá reálná proměnná, kterou je x. Tuto funkci označujeme jako funkci jedné reálné proměnné.
Ve fyzice fungují funkce stejně, představme si závislost rychlosti zrychlujícího tělesa na čase od počátku zrychlování:
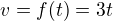
Důležité je, abychom si uvědomili, že nemusíme používat písmenka x a y, můžeme zvolit libovolná písmena abecedy.
Ve fyzice má každá veličina své označení – písmeno. Co to taková veličina je? Fyzikální veličinou myslíme obecnou vlastnost hmoty či energie (pro začátek si tyto dva pojmy rozdělme). Jak napovídá název, veličina musí mít nějakou velikost. Ty, které mají pouze velikost, označujeme jako veličiny skalární. Existují však i veličiny, které kromě velikosti mají i směr, jenž je dán vektorem. Ty označujeme jako veličiny vektorové. Tyto dva druhy budou pro náš kurz stačit.
Každá veličina se skládá ze dvou částí – velikosti a jednotky. Veličina X má velikost {X} a jednotku [X], zapisujeme: X={X}[X]. Uveďme si příklad:
Jednou z nejzákladnějších fyzikálních veličin je dráha. Dráha se značí písmenem s. Můžeme tedy napsat, že s={s}[s]. Jednotky dráhy jsou metry, tedy [s]=m, takže můžeme napsat, že s={s}m, kdy {s} je velikost – počet metrů.
Na světě existuje spousta veličin, avšak pouze sedm z nich je základních. Označujeme je za základní veličiny soustavy SI. Soustava SI je překlad z francouzského Le système International d’Unités (mezinárodní soustava jednotek). Proč hovořím o veličinách, ale mluvím o systému jednotek? Je to prosté, veličinu si můžeme pojmenovat, jakkoliv chceme, avšak velikost jedné její jednotky, to je něco, co musíme určit. Mikroskopicky se každé pravítko liší, jak bychom tedy mohli zachovat pevnou velikost metru? Musí existovat určitý standard a právě tento standard přináší mezinárodní soustava jednotek. Následující tabulku si dobře zapamatujte (definice uvedu jen u jednotek, u kterých si myslím, že je to důležité – definice si obecně pamatovat nemusíte):
| Fyzikální veličina | Základní jednotka | Definice základní jednotky |
|---|---|---|
| Dráha (s) | Metr (m) | Dráha, kterou urazí světlo za 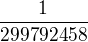 s. s. |
| Hmotnost (m) | Kilogram (kg) | Pevně daná hmotnost předmětu, který je uložen v Mezinárodním úřadě pro váhy a míry ve Francii. |
| Čas (t) | Sekunda (s) | Jedna sekunda trvá 9 192 631 770 period záření, které odpovídá přechodu mezi dvěma jemnými vrstvami atomu Cesia 133. |
| Termodynamická teplota (T) | Kelvin (K) | 0 K je absolutní nula, 273.16 K je teplota trojného bodu vody. |
| Elektrický proud (I) | Ampér (A) | |
| Svítivost (I) | Kandela (cd) | |
| Látkové množství (n) | Mol (mol) |
Všimněme si hned na začátku, že označení svítivosti a elektrického proudu je stejné. S tímto problémem se setkáme častěji v následujících lekcích. Důležité je, abychom si uvědomili, že písmena jsou pouze zástupci daných veličin, důležité jsou velikosti a jednotky veličiny – podle nich poznáme, o kterou veličinu se jedná.
Jednotky ostatních veličin
Jednotky veličin, které nejsou základními veličinami dle soustavy SI, můžeme pojmenovat – v praxi se to také děje. Vezměme si za příklad rychlost. Průměrnou rychlost na určité dráze definujeme jako délku této dráhy v závislosti na čase:
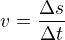
Jednotku rychlosti zjistíme tak, že dosadíme v základních veličinách libovolnou velikost, avšak počítáme s jednotkami:
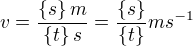
Poznámka autora: Velké řecké písmeno delta značí změnu (velké písmeno delta je trojúhelníček s cípem nahoře). Změna času kupříkladu znamená, že vezmu čas, kdy jsem přestal měřit a odečtu od něj čas, kdy jsem měřit začal, tím získám čas, po který jsem měřil. Příkladem nechť je toto:
Začátek měření 13:10, konec měření 14:35. Doba měření je tedy 14:35 - 13:10 = 1:25. Měřil jsem tedy hodinu a dvacet pět minut.
Jednotky rychlosti jsou tedy metry za sekundu. Všimněme si, že jsem zapsal 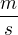 jako
jako 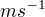 . Ve sbírkách příkladů se preferují zápisy s násobky a mocninami. Pomocí základních jednotek můžeme zapsat jednotku jakékoliv veličiny!
. Ve sbírkách příkladů se preferují zápisy s násobky a mocninami. Pomocí základních jednotek můžeme zapsat jednotku jakékoliv veličiny!
Jednotky mezi sebou můžeme násobit, sčítat apod. stejně jako proměnné.
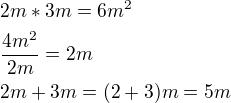
Co je třeba znát z matematiky?
Určitě se neobejdeme bez funkcí, jak jsme již na začátku řekli. Funkce se budu snažit vypisovat tak, aby se chovaly jako funkce jedné reálné proměnné – i když bude v obecné rovnici více proměnných, můžeme některé považovat za konstanty. Kupříkladu při měření rychlosti - řekli jsme si, že měříme na určité neměnné dráze, proto nás zajímá pouze čas jako proměnná.
Osobně budu pracovat i s výpočty pomocí derivací a integrálů, není však nutné, abyste tuto látku znali – některé odvozené vzorce si prostě budete muset pamatovat nebo si je někam zapsat. Maturant z fyziky by však měl být schopen si všechny vzorce sám odvodit a také by měl být schopný pracovat se základy diferenciálního a integrálního počtu. Pro ostatní je to, osobně si myslím, zbytečné.
Další věc z matematiky, která se hodí, je znalost goniometrie a goniometrických funkcí, zde není třeba přemýšlet, proč musíte danou látku zvládat, goniometrické funkce prostě používat budeme – střídavý proud, kmitavý pohyb, pohyb po kružnici…
Stejně tak je třeba znát logaritmické a exponenciální rovnice. Neunikneme jim kupříkladu u jaderné fyziky.
Další věcí je úprava výrazů, dosazování a vyjadřování proměnných. Často si vyjadřováním a dosazováním ušetříme práci se zapamatováním čísel.
A více toho myslím není třeba znát. :-)
Co navíc?
Podle ohlasů z prvního článku jsem se rozhodl, že do některých částí svých materiálů zkusím zapojit i něco o počítačovém pohledu na fyziku. Z mého pohledu to bude více méně matematická záležitost, kterou si může každý vložit do svého „kompjůtru“, aby si užil. Bude se jednat především o vykreslování grafů – řeknu vám, jaké matematické podmínky by měl takový graf splňovat, vy si pak můžete takový graf jakkoliv vytvořit – klidně interaktivní, kde bude i vidět, jak těleso padá apod. Mimo grafy se v programování dá vytvořit jakákoliv tabulka se vstupními informacemi, kterou později můžeme vykreslit – a poté můžeme náš problém (rovnici apod.) opět propojit s grafem, který nám bude vykreslovat to, co po něm budeme žádat.
Pro příznivce počítačového modelování mám možná dobrou zprávu, měl bych mít na škole jako předmět informatiku pro fyziky, takže až zde budu hotov se základní fyzikou, rozhodně rád přidám další informace o modelování situací a měření – popřípadě simulacích a bůh ví, čeho všeho – co všechno se naučím.
Co si odnést z tohoto dílu?
- Co je to fyzikální veličina a fyzikální jednotka.
- Základní veličiny a jednotky soustavy SI + co je to soustava SI.
- Odpověď na otázku: „Jaký matematický aparát potřebuji?“
- Pracování s jednotkami.
Úkol
Úkol pro tento díl kurzu bude, alespoň si myslím, velice jednoduchý. Bude se jednat o tři matematické rovnice, kdy máte vždy určit hodnotu proměnné, která se nachází v rovnici. Tedy hurá do toho.
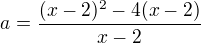
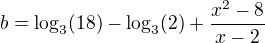
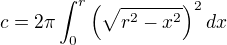
 TIP: Přetáhni ikonu na hlavní panel pro připnutí webu
TIP: Přetáhni ikonu na hlavní panel pro připnutí webu






