První skutečně fyzikální díl našeho kurzu je na světě! Začneme s tím, co považujeme ve fyzice za nejsnazší - mechaniku hmotného bodu. Tento článek má tři cíle: říci si, co je to kinematika a hmotný bod; seznámit se s dráhou, pozicí, rychlostí, zrychlením, úhlovou rychlostí a úhlovým zrychlením; odvodit základní vztahy mezi zrychlením, rychlostí a uraženou dráhou.

Jelikož je pojem mechanika vcelku snadný na vysvětlení, nemá smysl psát pro něj vlastní článek. V tomto článku tedy v rychlosti vysvětlím, co je to kinematika, dynamika, mechanika a hmotný bod - a vše s tím související.

Základní pojmy

Mechanika, kinematika, dynamika

Mechanika nemá nic společného s opravováním, po našem kurzu z vás tedy rozhodně nebude mechanik. :-) Mechanika je součást fyziky, která popisuje pohyb. Mechanikou hmotného bodu tedy myslíme část fyziky, která popisuje pohyb hmotného bodu.

Mechaniku můžeme rozdělit na dvě části - kinematiku a dynamiku. Kinematika nám popisuje průběh pohybu - ukazuje nám, jak rychle se těleso pohybuje, jak se v průběhu pohybu mění jeho rychlost, zrychlení a jakou dráhu těleso urazí. Dynamika oproti tomu zkoumá, proč se těleso hýbe v určitém směru. Má tedy na starost důvody změny či stálosti pohybu. Předem říkám, že kinematika je s dynamikou úzce spjata, přestože náš kurz je rozdělí.

Hmotný bod

Hmotný bod je bezrozměrný bod, kterým si nahrazujeme těleso v pohybu. Děláme to, abychom vyloučili (zanedbali) rozměry tělesa, tudíž i odporové síly (viz dynamika). Jelikož je bod "hmotný", tak si zachová svou hmotnost, což je důležité. Časem se od hmotného bodu odpoutáme, avšak pro začátek ho budeme používat jako pohybující se bod, jehož dráhu popisujeme. Takový bod si můžeme představit jako velice malý míček, který se pohybuje.

Kinematika hmotného bodu - veličiny

Abychom začali popisovat pohyb, musíme si zvolit určité veličiny - co je to veličina se dozvíte ve druhém díle kurzu (co je třeba znát? [ http://programujte.com/clanek/2011090200-stredoskolska-fyzika-zacatek-co-je-treba-znat/ ]).

Souřadnice

Abychom mohli těleso nějak nalézt v prostoru, musíme určit jeho souřadnice. Souřadnice jako takové ještě nejsou veličiny, ale budeme je často používat - příkladem nechť je pohyb po kružnici.

V našem prostoru známe čtyři souřadnice, kterými můžeme popsat těleso. Tyto souřadnice jsou x, y, z, t. První tři souřadnice nám udávají, kde se těleso nalézá, poslední souřadnice nám udává, kdy se těleso nalézá. Dohromady nám tedy tyto čtyři souřadnice řeknou, kde a kdy těleso je, což nám bohatě stačí. Souřadnice x, y, z jsou kartézské souřadnice, které používáme pro orientaci v prostoru. Souřadnice t je veličina a popíšeme si ji v dalším odstavci.

Za zmínku stojí i to, že mimo kartézské souřadnice jsou praktické i souřadnice polární. Já polární souřadnice používat nebudu, jelikož si myslím, že kartézské nám bohatě stačí. S polárními souřadnicemi se setkáte kupříkladu v trigonometrickém tvaru komplexního čísla.

Čas

Čas značíme t (z anglického time). Je to veličina, která nám říká, v jakém okamžiku se co děje. Stejně jako je lidstvo závislé na čase, tak je na něm závislá i většina mechaniky.

Základní jednotkou času jsou sekundy (s), sekundy jsou základní jednotkou SI.

Dráha

Dráha souvisí se souřadnicemi tělesa, které sledujeme. Pokud se těleso pohybuje po ose x a změní za určitý čas svou pozici z x = 5 m na x = 7 m, poté říkáme, že urazilo 2 metry.

Základní jednotkou dráhy jsou metry (m) a značíme ji s. Metry jsou základní jednotkou SI.

Rychlost

První veličinou, která je definována pomocí jiných veličin, je rychlost. Rychlost nám říká, jak "rychle" se těleso pohybuje. Průměrná rychlost na určitém úseku je definována jako změna dráhy za změnu času:

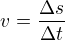
Pokud si představíme jedoucí auto, tak abychom získali jeho aktuální, ne průměrnou rychlost, budeme se snažit měřit jeho rychlost na co nejmenším časovém úseku. Stále to však bude průměrná rychlost na takovém časovém úseku. Matematicky tedy řekneme, že abychom dostali aktuální rychlost bodu/tělesa/auta, musíme změnu času nechat se limitně blížit k nule - délku časového úseku k nule:

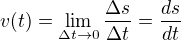
Jak si všimneme, tento zápis se rovná derivaci funkce dráhy podle proměnné času. Z tohoto vztahu velice jednoduše přejdeme do vztahu závislosti dráhy na čase, který v dalším dílu využijeme:

Všimněme si tedy, že - vcelku logicky - pokud je funkce dráhy v závislosti na čase integrálem rychlosti podle proměnné času, znamená to, že funkce aktuální rychlosti je derivací funkce dráhy. Pro nás tento výsledek znamená, že pokud chceme změnu dráhy na určitém úseku, neurčitý integrál nám stačit nebude. Abychom si mohli správně odvodit změnu dráhy na určitém úseku, budeme potřebovat integrál určitý, bude tedy platit:

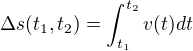
Následně vidíme určený integrál i graficky (graf nám ukazuje obsah plochy, která je rovna velikosti dráhy, kterou těleso urazí - graf, jak je vidět, je grafem závislosti rychlosti na čase):

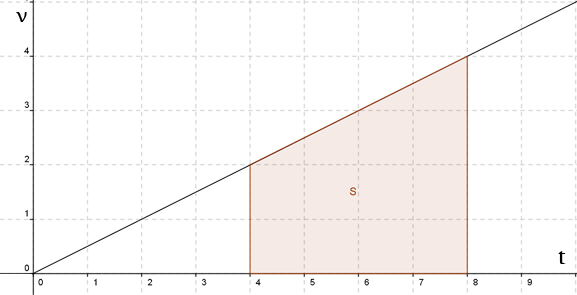
Zrychlení

Zrychlení - akcelerace - pochází z anglického slovíčka Acceleration, což doslovně znamená právě zrychlení. Značka zrychlení tudíž nikoho nepřekvapí - a.

U zrychlení platí ty samé vztahy, které platí u rychlosti, pouze se použije jiná veličina. Základní definice průměrného zrychlení na určitém časovém úseku je taková, že je to změna rychlosti za změnu času:

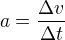
Další vztahy následují dle stejného pravidla, které jsme si říkali u rychlosti, pouze "v rychlosti" je tedy sepíšu pod sebe:

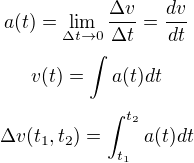
Za zmínku stojí, že zrychlení rozdělujeme na dvě složky (dle vektorového součtu). První nazýváme zrychlení tečné, které zajišťuje změnu velikosti rychlosti, druhé nazýváme zrychlení normálové, které zajišťuje změnu směru rychlosti. Jelikož jsou zrychlení i rychlost vektorové veličiny, znamená to, že změna rychlosti může znamenat i změnu směru, nejen velikosti.

Úhlová rychlost

Následující veličiny (úhlovou rychlost a úhlové zrychlení) budeme používat pouze u křivočarého pohybu. Ne snad proto, že by se u přímočarého pohybu nedaly použít, avšak jsou vždy rovny nule, jelikož úhel jakéhokoliv vektoru, který se na přímce dá vytvořit, je vůči jakékoliv ose vždy stejný - je-li osa pevně daná.

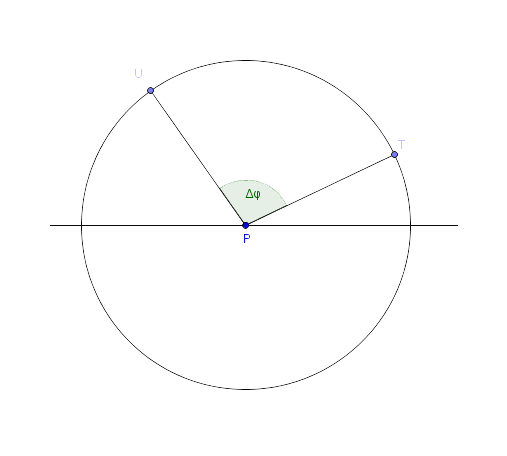
U každého křivočarého pohybu zjišťujeme, jak se mění úhel v závislosti na čase. Obecný vzoreček je tedy:

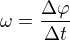
Stejně jako u rychlosti a zrychlení dojdeme ke vztahu pomocí derivací:

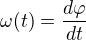
Abychom přesně věděli, co to znamená změna úhlu, ukážeme si to na následujícím obrázku. Vidíme, že v čase je bod na jiném místě než v čase 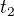. Úsečka, která spojuje bod P a T, se nazývá průvodič. Stejně tak je průvodičem úsečka PU.

Úhlové zrychlení

Stejně jako se může měnit rychlost tělesa a její směr, může se měnit velikost úhlové rychlosti. Krásným příkladem nechť je kometa, která obíhá okolo Slunce po elipse. Čím blíže je kometa, tím větší má úhlovou (i normální) rychlost a opačně.

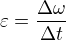
Závěr

Myslím si, že všechny základní vztahy jsme si již odvodili, v příštím díle už je můžeme vesele používat, díky čemuž si odvodíme pár vzorců, ukážeme si grafy závislostí dráhy a rychlosti na čase nebo grafickou závislost.

Úkol (lekce č. 1)

Za úkol v tomto dílu, který ještě není tolik konkrétní, budu chtít, abyste mi přiblížili jeden pojem, který jsem zde uvedl. Rád bych věděl, co je to elipsa a jestli je kružnice elipsa...?

Není to nakonec nic těžkého, takže k tomu ještě přidám jednu otázku. Pokud se těleso pohybuje po elipse a jeho rychlost v je konstantní, bude se v průběhu měnit úhlová rychlost? Zkuste se nad tím zamyslet, dobrý začátek bude nakreslit si elipsu.

Pro ty, kteří by se nudili, tak jsem schválně neřekl vztah mezi změnou úhlu fí a změnou času, co se týče úhlového zrychlení. Napište mi tedy vzorec pro úhlové zrychlení pomocí fí a t. :-)