Tento díl věnuji studiu křivočarých pohybů. V minulém díle jsem byl upozorněn na fakt, že jsem provedl výklad příliš nesrozumitelně, dokonce jsem byl nařčen, že opisuji skripta. Pokusím se tedy v tomto díle být "přímočařejší" (přestože se jedná o křivočaré téma :) ) a budu doufat, že si nikdo nebude myslet, že své články přepisuji ze skript.
V minulém dílu jsme si ukázali, jak na přímočaré pohyby. Nyní bychom se měli zaměřit na pohyby křivočaré.
Křivočarý pohyb obecně znamená, že jeho trajektorií není rovná čára, ale nějaká čára křivá, jak se dá vyčíst z názvu. Nemůžeme již tedy mluvit o pohybu po přímce, avšak musíme se věnovat pohybu, který probíhá po nějaké ploše či přímo v prostoru. Takový pohyb udáme parametrickým vyjádřením tří jeho kartézských souřadnic:

Je dobré si uvědomit, jak by tyto parametrické rovnice vypadaly v rámci přímočarého pohybu. Budeme-li mít pevně daný počátek soustavy souřadnic a osy x, y, z, potom budeme přímočarý pohyb sledovat i v případě, že se budou měnit hodnoty všech souřadnic bodu [x,y,z].
Aby se jednalo o přímočarý pohyb, musí pro každou ze souřadnic platit, že jsou na parametru t závislé "stejnou mírou". Ukažme si odvození, pomocí kterého se dostaneme v ploše k obecnému tvaru přímky. Obecně platí, že máme-li každou souřadnici vyjádřenou rovnicí, která je polynomem nejvýše prvního stupně, pak se jedná o přímočarý pohyb. Polynom nejvýše druhého stupně znamená přítomnost členů "a + bt" nebo pouze konstantního členu "a".
Nyní si ukažme pro plošný pohyb, že máme-li vyjádření dvou stejných funkcí f(t) různých od nuly, platí, že se jedná o pohyb po přímce.

Dostali jsme rovnici přímky s koeficienty b, -a, 0.
Nyní zpět ke křivočarým pohybům.
Existuje několik speciáních druhů pohybů, které si můžeme popsat jednoduše pomocí středoškolské matematiky. Prvně si však zopakujeme a možná prohloubíme něco o zrychlení. Už víme, že rychlost je vektorem, to znamená, že kromě velikosti má i směr. Zrychlení si rozdělme na dvě části.
První nechť je zrychlení tečné. Toto zrychlení má směr tečny k trajektorii pohybu (stejný směr jako rychlost). Druhou nechť je zrychlení normálové. Normálové zrychlení má směr normály k trajektorii. Sečteme-li obě tato zrychlení, dostaneme zrychlení celkové. To znamená, že libovolné zrychlení můžeme rozložit na tečnou a normálovou složku.
A proč je to dobré? Každá složka zrychlení totiž ovlivňuje jinou vlastnost rychlosti. Tečná složka zrychlení ovlivňuje velikost rychlosti, normálová složka ovliňuje její směr.
U přímočarých pohybů, které jsme probírali v minulém díle, je tedy normálové zrychlení nutně nulové.
Nyní se pojďme podívat na speciální křivočaré pohyby.
Rovnoměrný pohyb po kružnici
Už z názvu je nám jasné, že máme-li rovnoměrný pohyb po kružnici, bude jeho rychlost konstantní a trajektorií takového pohybu bude kružnice.
Takové rovnice zapíšeme v nejsnazší formě jako

Budeme-li chtít spočítat trajektorii bodu, vyloučíme hodnotu parametru úhlu z rovnic. Dáme obě rovnice na druhou a sečteme je.

Vidíme, že dostáváme středovou rovnici kružnice o poloměru r.
Jelikož se velikost rychlosti nemění, tak musí platit, že tečné zrychlení je nulové. Oproti tomu zrychlení normálové musí být konstantní. K jeho velikosti se ještě dostaneme v podčásti dostředivé zrychlení.
Začněme tím, že řekneme, že uražená dráha za nějaký čas je rovna dle matematické teorie
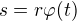
a jelikož víme, že rovnoměrný pohyb po kružnici má stejnou obvodovou rychlost, snadno vytvoříme úvahu, že úhel se v čase mění stále stejnou rychlostí. Nechme však tuto úvahu ještě chvilku ležet.
Nyní se pokusíme vyjádřit obvodovou rychlost dle standartní definice rovnoměrného pohybu. Jelikož se zabýváme pouze velikostí rychlosti a ne jejím směrem, můžeme napsat následující vztah:
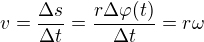
Vidíme tedy, že za předpokladu konstantní rychlosti a stálého poloměru kružnice musí být i úhlová rychlost konstantní. Z toho vyplývá, že musí být konstantní i úhel uražený za stejný čas v různých počátečních okamžicích. Tímto jsme si potvrdili svou úvahu z odstavce o několik řádek výše.
Poznámka navíc z VŠ: Lehkým ověřením bychom dostali, že tečné zrychlení je nulové - stačí zderivovat poslední odvozený vztah podle času.
Je-li konstantní úhlová rychlost, znamená to pro nás nulové úhlové zrychlení. To si můžeme odůvodnit tím, že derivace konstanty je nula, nebo úvahou, která spočívá v tom, že je-li úhlová rychlost stále stejná, logicky se nemůže zmenšovat ani snižovat (přímo z definice průměrného úhlového zrychlení).
O úhlových veličinách (funkce úhlu, úhlové rychlosti a úhlového zrychlení) jsme si již vše řekli. Také jsme si řekli, jak vypadá dráha uražená tělesem a její aktuální rychlost v závislosti na čase. Chybí nám tedy už jen poslední veličina, kterou můžeme odvodit, a tou jest dostředivé zrychlení.
Dostředivé zrychlení je možná nejdůležitější věcí této kapitoly - využívá se především v dynamice, kde se řeší dostředivá (popř. odstředivá) síla, pomocí níž můžeme určit kupříkladu první kosmickou rychlost, ale k tomu až později.
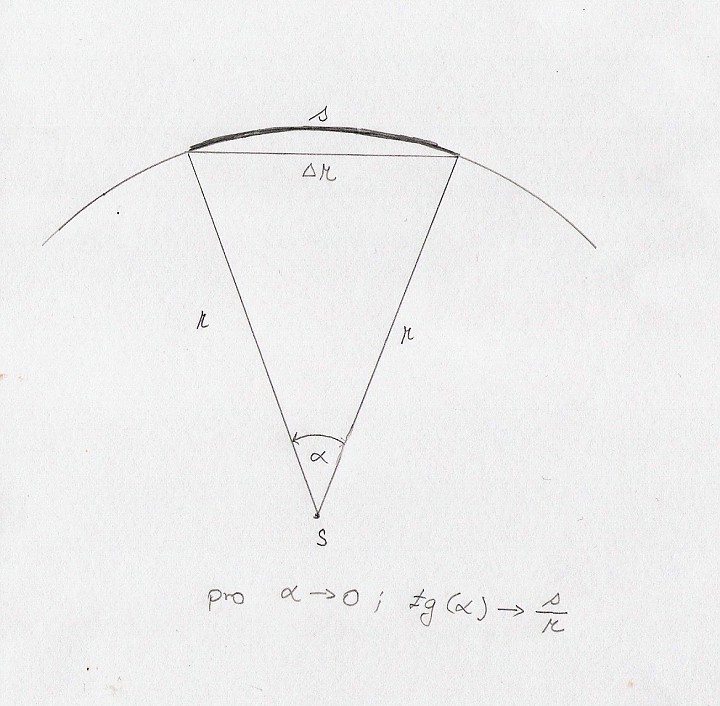
Dostředivé zrychlení je normálové zrychlení pohybu, jak jsme si již řekli. Toto zrychlení způsobuje, že vektor rychlosti mění svůj směr. Jak určit hodnotu tohoto zrychlení? Vycházejme zatím z toho, jak je situace nakreslena na obrázku 1.
Vidíme, že platí vztah

a stejně tak dle obrázku 2
platí vztah
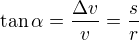
z čehož můžeme vyjádřit změnu rychlosti jako

Nyní vyjděme z definice zrychlení. Zrychlení je rovno změně rychlosti za nějaký čas, dostáváme tedy vyjádření, které můžeme snadno přepsat následujícím postupem:

Ať už vyjádřením pomocí rychlosti, nebo úhlové rychlosti, dostáváme vztah pro dostředivé zrychlení, které pro nás bude časem důležité.
Poznámka: V obrázku je použit zápis pro limity funkcí. Pro ty z vás, kteří limity neznají, vězte, že obrázek s rychlostí je jasný a pro obrázek se změnou poloměru r a uraženou dráhou s vystihuje, že čím menší bude úhel alfa, tím více se bude s rovnat změně r, tedy pro velice malé úhly nastane téměř stoprocentní rovnost. Nevěšte hlavu, jestli nerozumíte proč, časem se to dozvíte - nicméně vzorce nejsou přibližné, ale přesné.
Libovolný křivočarý pohyb má určité normálové zrychlení. V praxi ho uvažujeme jako dostředivé zrychlení oskulační kružnice. Oskulační kružnici či též kružnici křivosti, jak se jí říká, si můžeme představit jako takovou kružnici, která svým tvarem nejlépe kopíruje trajektorii pohybu v daném bodě. Veličinu r poté nenazýváme poloměrem kružnice, ale poloměrem křivosti oskulační kružnice.
U pohybu po kružnici ještě používáme veličiny peroidu oběhu T, frekvenci oběhu f a zabýváme se vztahy mezi nimi a vztahy vůči ostatním veličinám.
Periodou oběhu myslíme dobu, za kterou bod oběhne celou kružnici a vrátí se do stejného místa, ve kterém "startoval". Hodnota frekvence oběhu nám udává, kolikrát bod obkrouží kružnici za jednu sekundu. Není těžké si uvědomit, že mezi těmito dvěma veličinami bude platit vztah
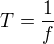
Následující vztah uvedu bez odvození, měl by jej znát každý. Kdo chce, může si ho zkusit odvodit. Přidám nápovědu, že uvažujeme, jaký úhel urazí těleso za určitou dobu, když tou dobou bude perioda oběhu (není to nic složitého).
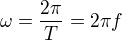
A tímto můžeme skončit rovnoměrný pohyb po kružnici.
Rovnoměrně zrychlený pohyb po kružnici
Povídání o rovnoměrně zrychleném pohybu po kružnici není příliš středoškolskou látkou, přesto však není tak náročné, aby ho středoškolák před maturitou nepochopil. Kvůli proměnlivosti pohybu zde již hrají větší roli derivace. Pomocí derivací a integrálů budu řešit několik příkladů.
Poznámka: Minule jsem byl hnán právě za užití derivací a integrálů. Aby nedošlo k podobným incidentům, tak vysvětlím, jak přistupovat k následující kapitole. Je-li čtenář úplný začátečník a matematice, kterou používám, nerozumí a zároveň nechce znát něco navíc, nechť si tuto část článku vůbec nečte. Je-li čtenář zběhlý v matematice a zná diferenciální a integrální počet, může si číst dle libosti. A ve finále ti, kteří se chtějí něco dozvědět, přestože nerozumí derivacím a integrálům, nechť si tuto část článku přečtou - to, že nerozumíte matematice, nutně neznamená, že nebudete rozumět ani fyzice.
Uvažujeme tedy konstatní úhlové zrychlení pro pohyb po kružnici. Z toho vyplývá hned několik následujících vztahů:
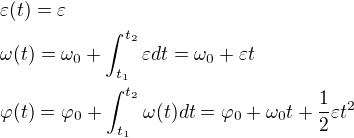
Všimněme si analogie s přímočarým rovnoměrným pohybem, kde místo úhlového zrychlení a úhlové rychlosti máme klasické zrychlení a klasickou rychlost. Místo aktuální polohy máme aktuální hodnotu úhlu. Je logické, že pokud se bude zvyšovat lineární úhlová rychlost, musí se lineárně zvyšovat i oběhová (tečná) rychlost, aby se bod udržel na kružnici, při tomto pohybu již tedy není tečné zrychlení nulové!
Jak určit dráhu uraženou tělesem? V předchozím případě jsme uvažovali, že změna úhlu je konstantní funkcí, nyní místo této konstantní závislosti dosadíme funkci pro úhel:
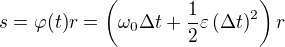
Perioda oběhu nebo frekvence nás při tomto pohybu zajímat nebude.
 TIP: Přetáhni ikonu na hlavní panel pro připnutí webu
TIP: Přetáhni ikonu na hlavní panel pro připnutí webu