a
Fórum › Pascal
Kartezsky soucin dvou mnozin realych cisel

#1 fak.gesho
Ahoj,
potreboval bych vytvorit 2 mnoziny realnych cisel (z intervalu -1,1), prvni interval jako <-1; -1+(2/37); -1+2*(2/37);...;1> a druhy stejny jen rozdeleny cislem (2/73) a pote bych potreboval jejich kartezsky soucin jako vstup pro funkci dvou promennych. Lamu si stim hlavu uz dlouho a absolutne nevim jake datove typy zvolit.
Dik
tady bych to videl klidne na dva cykly ... vypocitat x,y dosadit do funkce... a vypsat +/- ...
muzes dokonce pouzit i for.. od 0 do 72 a z toho vypocitat hodnoty a na radky od 0 do 32 .. (radky budou mit ten sloupcovy cyklus uvnitr.. nic tezkeho)
No, ty hlavně ten interval podle mě musíš diskretizovat, tzn tu X-osu, Y-osu musíš rozdělít na 37 resp 73 ekvidistatních bodů
x = {-1, -0,98.., - 0,97.., x, x, x, ....atd... } -- y = {to uz víš}
a z téhle množiny budeš volit souřadnce pro dosazování.. => Kartézský součin nad těmy množinami bude generovat tu síť (souřadnicovou)
Tenhle algo je to co popsal KIIV .. měl jsem to už napsaný, když jsem si všimnul že to napsal :D
For i:=0 to 37 do
begin
For j:=0 to 73 do
begin
x:=-1+i*(1/37);
y:=-1+j*(1/73)
if((67039*power(x,12)-1939938*power(x,10)
-184756*power(y,10)...atd...)>0) then
begin
write("+");
end;
else write("-")
end;
writeln;
end;
end;
Omlouvám se za můj pascal, dělal jsem v něm naposledy na střední, což je už nějakej tejden, ale myslím že by tohle mohlo běžet .. s tím že power je v knihovně Math (asi)
Fakulta aplikovaných věd www.fav.zcu.cz
"Když nedokážete říci věci jednoduše, pak jim dostatečně nerozumíte"
tak jestli to funguje je to ok.. ale mam tuseni ze mozna jedes jen v intervalech od <-1;0>, protoze -1+ j*(1/73) kde j je od 0 do 73 (coz je 74 hodnot - 74 sloupcu) mas minumum -1 a maximum je -1+1 = 0 tj. do jednicky ti jeste neco malo chybi
+ v tom kodu je spousta dalsich chybicek.. treba 0 se ma brat tez jako kladne
ano, jsou tam drobne chybicky, ale po prepsani to opravdu vraci presne stejnou tabulku. deklaroval jsem si promenne x a y jako realna cisla (a tam to omezeni neni, takze jedou podle poctu kroku do 36 or 72) a prepsal jsem delku intervalu (abych mel ve vysledku 37 hodnot a ne 38, stejne tak 73 nq 72 ) a prohodil promenne.
 Zjistit počet nových příspěvků
Zjistit počet nových příspěvků
Přidej příspěvek
Ano, opravdu chci reagovat → zobrazí formulář pro přidání příspěvku
×Vložení zdrojáku
×Vložení obrázku
×Vložení videa
































Uživatelé prohlížející si toto vlákno
Podobná vlákna
Průnik dvou množin — založil vasek230
Prohození dvou čísel — založil Michal
Součet dvou binárních čísel — založil Dalibor
C# Načtení dvou čísel ze vstupu — založil Genom
Násobení dvou náhodných čísel — založil k2k21
Moderátoři diskuze
 TIP: Přetáhni ikonu na hlavní panel pro připnutí webu
TIP: Přetáhni ikonu na hlavní panel pro připnutí webu



 Nahlásit jako SPAM
Nahlásit jako SPAM IP: 82.142.125.–
IP: 82.142.125.– God of flame
God of flame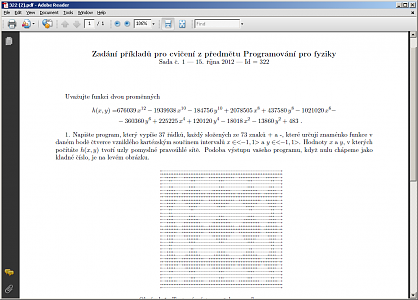
 Super člen
Super člen

