
Dříve než budu rozebírat další věci, bude dobré (také díky zpětné vazbě, kterou mi poskytli čtenáři) více osvětlit některé postupy, které jsem použil v úvodním článku. Umožní to lépe porozumět pozadí a podstatě fungování.
Na několika místech jsem zacházel s přiřazením přímo jako s rovnicí. Není to jen nějaký pochybný trik, o rovnicích jsem psal záměrně, má to své důvody.
To, jak s kódem v těchto článcích zacházím, závisí na kontextově vhodné definici přiřazení. Pojem přiřazení souvisí s pojmem proměnná. Myslím si, že bývají užívány značně omezeně a učebnice se spoléhají spíše na zažité definice typu proměnná je místo v paměti. Proměnná je ale víc než to.
Přiřazení
Představuju si, že úplně poprvé prohlížím nějaký zdrojový kód.
Na jednom řádku je tam napsáno x = x + 3.
Pomyslím si: „Hele to znám, to je rovnice…“
O chvilku později:
„...ale počkat! To je nějaký nesmysl, kdybych odečetl x dostanu 0=3, přece třeba 5 mrkví se nerovná 5 mrkví + 3 mrkve, to nebude rovnice…“
Později se dozvídám, že se takhle zapisuje tzv. přiřazení, přiřazovací příkaz. Přiřazovací příkaz znamená, že se nejprve spočítá (vyhodnotí) to, co je napravo od znaku rovná se, a výsledek se strčí do proměnné nalevo od znaku rovná se. Na levé straně musí být tzv. L-hodnota, která zastupuje konkrétní místo v paměti, do něhož se výsledek zapíše.
Zdá se, že přiřazovací příkaz je něco trochu jiného než rovnice, považovat jej přímo za rovnici vede k nesmyslům.
Zajímavé je, jak syntaxe některých programovacích jazyků přímo naznačuje, že přiřazení je něco trochu jiného než rovnice. Basic dříve používal zápis LET X = X + 3, Pascal používá zápis x := x + 3, Cčkové jazyky to umožňují zapsat dokonce zkráceně x += 3. Významově mi ty zápisy trochu připomínají Assembler, ve kterém by se použil příkaz/instrukce: ADD X, 3.
Co tím chci říct
Významem zápisu myslím, že je to rozkazovací, tzv. imperativní úhel pohledu na věc. Existuje i jiný, říkejme mu třeba popisný úhel pohledu, kdy to jsou rovnice a ne příkazy. A takto se dívat na věc má své výhody, popisný přístup je na vyšší úrovni abstrakce než imperativní (viz ten Assembler).
Jaký je ale skutečný vztah pojmu přiřazení a rovnice? Abychom to zjistili, podívejme se, co se při přiřazení skutečně děje.
Přiřazení x = x + 3 můžeme rozložit do více kroků:
r = x; // Načtení současné hodnoty x do r
w = r + 3; // Výpočet
x = w; // Uložení nově vypočtené hodnoty do x a tím tak
// přepsání/zahození původní hodnoty x
r a w jsou dočasné proměnné, zpočátku nedefinované.
Vidíme, že v prostředním řádku je už korektní rovnice. A taky poslední řádek přepisuje/zahazuje původní hodnotu x. Může se zahodit proto, že už není pro další postup programu potřeba. Přepsáním ale ztrácíme informaci o původní hodnotě proměnné, právě proto se zdráháme pracovat s ním přímo jako s rovnicí.
Tohle je imperativní přístup - proměnná je konkrétní místo v paměti, jehož hodnota se mění (přepisuje). Jsou takto navrhovány procesory a vše okolo, protože z praktických nebo fyzikálních důvodů to ani jinak nejde. Takto se na dívat na věc je ale jen naše volba. Teoreticky si vše lze představit i jinak.
Ke ztrátě informace narušující rovnici nebude docházet, když si uvědomíme, že proměnnou nemusíme vždy brát jako místo paměti, jehož hodnota se přepisuje. Proměnnou si můžeme představit také jako seznam hodnot či pole, které s každou změnou proměnné roste, a současná hodnota proměnné je poslední položkou v poli. Zápis x = x + 3 je totiž určité zjednodušení, které se dá matematicky výstižněji zapsat takto: xt+1 = xt + 3, kde t je čas, pořadí změny proměnné. V analogii s polem je t nebo t+1 index hodnoty proměnné v poli (viz obrázek).
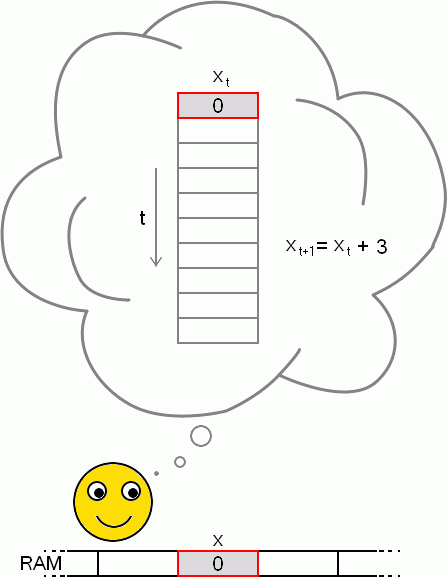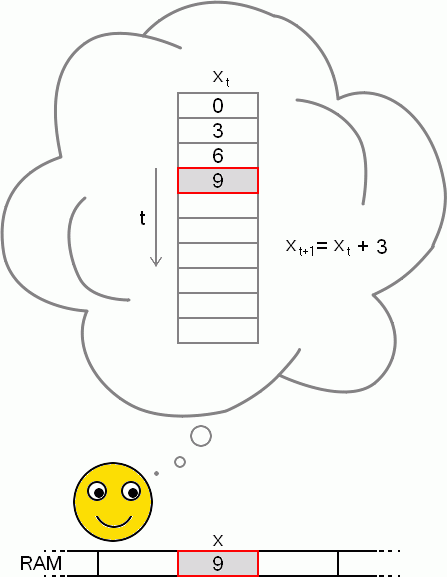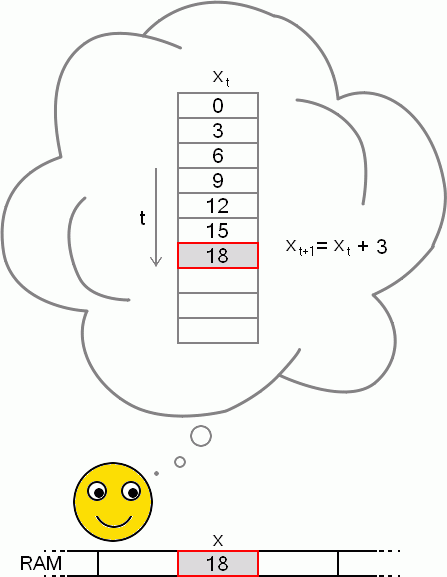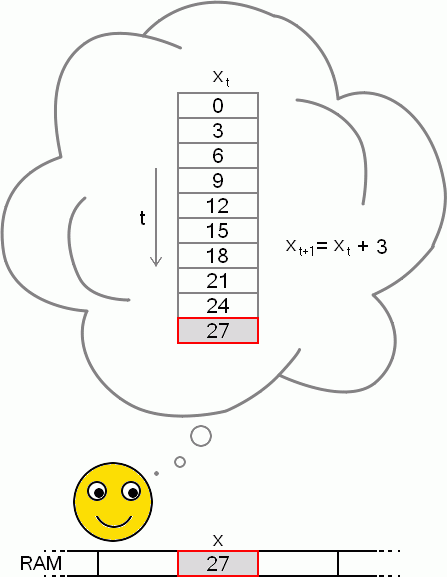
Ani už nemusíme mluvit o přiřazení, je to rovnice, s kterou můžeme obecně pracovat a vyjádřit si, co potřebujeme. Získáváme tím daleko větší volnost. Nejen že víme, jak nějaká hodnota závisí na předchozí, můžeme si třeba vyjádřit, jak hodnota proměnné závisí třeba na před-předchozí hodnotě apod.
Přiřazení/rovnice z předchozího článku
(x+3) = (x+3) + 1 pod povrchem znamená (xt+1 + 3) = (xt + 3) + 1, odečtu 3 od obou stran a dostanu xt+1 = xt + 1. Když si vyjádřím změnu dostanu xt+1 - xt = +1 a to je vlasně příkaz x++.
Většinou ale není potřeba rozebírat to tak podrobně, jde to často z hlavy. Když mám třeba (x+3) = (x+3) + 1, tak si uvědomím, že x na pravé straně není to samé x jako na levé a nemůžu je tedy od sebe odečíst a dostat 0. Jediné zjednodušení, co tady můžu provést, je odečíst trojku a dostanu x = x + 1.
Shrnutí - vztah pojmů přiřazení a rovnice
Přiřazovací příkaz je změna, co se má provést (rozkazuju). A rovnice je vztah, který platí mezi věcmi (popisuju). Mám-li určitý vztah, změnu (příkaz) si z něho můžu vyjádřit, je to jedna z jeho forem, a obráceně přiřazovací příkaz můžu zobecnit na vztah.
Závěr
Definice pojmu přiřazení a vůbec pojem samotný pochází z toho, jak je v imperativních programovacích jazycích implementována práce s proměnnými. Přiřazení je pojem jako určitý speciální případ obecnějšího pojmu rovnice upraveného, podřízeného implementaci.
Častokrát můžeme někde číst, že proměnná v programu je místo v paměti, „uložiště“ informace nebo vyhrazené místo v paměti atd. Prakticky je to tak a v článku jsem se pokusil trochu ukázat, že máme teoreticky i jinou možnost, jak to brát. To, že se nejčastěji programuje v imperativních programovacích jazycích, kde proměnná je nějaké místo v paměti, ještě neznamená, že o tom tak i v těchto jazycích musíme vždy přemýšlet…
Prosím hodnoťte článek, pište dotazy, názory, kritiku, nápady, svoje zkušenosti.
 TIP: Přetáhni ikonu na hlavní panel pro připnutí webu
TIP: Přetáhni ikonu na hlavní panel pro připnutí webu






