
V tomto díle budeme pokračovat pouze praktickými ukázkami. Na třech příkladech si znovu ukážeme použití polí. V prvním příkladu budeme generovat sloupek tiketu Sportky. V druhém příkladu budeme pracovat se školními známkami. A ve třetím příkladu si uděláme jednoduchou implementaci Eratosthenova síta.
Sportka
 Vytvořte algortimus pro generování jednoho sloupce tiketu Sportky (6 čísel ze 49 možných). Tentokrát vstupem uživatele nebude nic a výstupem bude 6 čísel, která počítač vybere.
Vytvořte algortimus pro generování jednoho sloupce tiketu Sportky (6 čísel ze 49 možných). Tentokrát vstupem uživatele nebude nic a výstupem bude 6 čísel, která počítač vybere.
Ke generování náhodných čísel použijeme generátor (pseudo)náhodných čísel, který je součástí každého vyššího programovacího jazyka. Problém takového generování je v tom, že se mohou opakovat stejná čísla, a to je věc, které musíme zabránit. Musíme si tudíž pamatovat již vygenerovaná čísla, abychom mohli zjistit, jestli už jsme je na (pomysleném) tiketu zaškrtnuli, nebo ne. K tomuto účelu nám dobře poslouží pole.
Definujeme si proto pole o velikosti 6, které bude obsahovat vygenerovaná čísla. Do pole se budou ukládat čísla 1 až 49, takže nám postačí nejmenší celočíselný datový typ (byte). Generovat čísla budeme v cyklu, a to do chvíle, kdy budeme mít všech 6 (nestejných) čísel, takže nepoužijeme cyklus s daným počtem opakování, ale cyklus s podmínkou na konci, protože tělo cyklu se musí vykonat minimálně jednou (resp. minimálně šestkrát). Po vygenerování čísla se musíme podívat, jestli už jsme takové číslo zaškrtli v tiketu (jestli je uložené v poli), a pokud ne, tak si ho uložíme a generujeme další číslo.
Výsledný vývojový diagram vidíte na obrázku. Před generováním čísel si musíme pole vynulovat. Vnějším cyklem kontrolujeme, jestli už jsme vygenerovali všech šest čísel, a vnitřním cyklem kontrolujeme, jestli číslo bylo nebo nebylo vygenerované. Po vygenerování čísel je před ukončením program ještě vypíše.
Poznámka: výstup nebude setříděný, ale čísla budou vypsána v pořadí, v jakém se vygenerují. Pokud bychom chtěli čísla na výstupu setříděná, tak to lze řešit buď tříděním, které bude náplní dalších dílů, nebo bychom na to šli bez třídění například přes pole 49 hodnot typu boolean.
Průměr a četnost známek
Se školními známkami se dají dělat různá kouzla anebo také příklady na algoritmizaci. Například takovýto: vytvořte algoritmus pro načtení a uložení zadaného počtu známek. Ze známek následně vypočítejte průměr a zjistěte jejich četnost.
 K uložení známek budeme potřebovat pole a protože budeme ukládat školní známky 1 až 5, tak nám opět stačí nejmenší celočíselný datový typ - byte. Zadaný počet známek může být velký, ale do 4 bajtů bychom se měli vejít, a proto můžeme použít třeba int. Stejně tak četnost známek může být velká - teoreticky mohou být všechny známky stejné, takže pro uložení četnosti známek si vytvoříme pole typu dword o délce 5 (je pouze pět známek).
K uložení známek budeme potřebovat pole a protože budeme ukládat školní známky 1 až 5, tak nám opět stačí nejmenší celočíselný datový typ - byte. Zadaný počet známek může být velký, ale do 4 bajtů bychom se měli vejít, a proto můžeme použít třeba int. Stejně tak četnost známek může být velká - teoreticky mohou být všechny známky stejné, takže pro uložení četnosti známek si vytvoříme pole typu dword o délce 5 (je pouze pět známek).
Nejprve musíme známky načíst do pole. Jejich počet nám zadá uživatel, takže velikost pole se bude dynamicky nastavovat (nebude známo před spuštením programu). Následně se v cyklu s daným počtem opakování, protože již víme, kolik těch známek bude, načtou známky do pole tak, jak je bude uživatel zadávat.
Ve druhé části budeme načtené známky zpracovávat. Opět k tomu použijeme cyklus s daným počtem opakování. Budeme počítat součet známek a budeme si i plnit pole četností známek. Před vstupem do cyklu si musíme pole s četnostmi vynulovat (zde možno i jednotlivě C[1] = 0, C[2]=0 atd. nebo, tak jako ve vývojovém diagramu, pomocí cyklu). Nakonec vypočítáme průměr. Vypočtený průměr vypíšeme, stejně jako zjištěné četnosti známek. Pro výpis všech pěti hodnot opět použijeme cyklus.
Pro počítání četnosti se používá "fígl", kde hodnota známky (1 až 5) se rovnou stává indexem do pole četností. Proto je zde použit zápis C[ A[J] ], tj. hodnota jednoho šuplíčku pole A na indexu J se stává indexem do druhého pole C. Samozřejmě lze provést zápis, kdy do nějaké pomocné T = A[J] si uložíme onu hodnotu a ta se stane posléze indexem do druhého pole - C[T]. Ve vývojovém diagramu je pro ukázku použit první (zkrácený) zápis.
Výsledný vývojový diagram vidíte na obrázku. Je zde explicitně uvedeno nastavení velikosti pole po její zadání uživatelem. Toto nastavení by se nemuselo uvádět, ale my si ho budeme do vývojových diagramů zapisovat vždy.
Poznámka: na výpočet průměru a zjištění četnosti jsme si známky ukládat nemuseli, šlo pouze o to, aby ukázka byla co nejjednodušší. V diagramu se nekontrolují zadané známky, neboť by byl již velmi dlouhý a nám jde o ukázku použití polí, jinak stále platí, že zadané hodnoty od uživatele je nutné kontrolovat. Vždy!
Eratosthenovo síto
 Eratosthenovo síto je jednoduchý algoritmus pro nalezení všech prvočísel menších než zadaná horní mez. My nebudeme na této jednoduchosti nic měnit, takže zadání by znělo úplně stejně: nalezněte všechna prvočísla do zadané horní meze metodou Eratosthenova síta.
Eratosthenovo síto je jednoduchý algoritmus pro nalezení všech prvočísel menších než zadaná horní mez. My nebudeme na této jednoduchosti nic měnit, takže zadání by znělo úplně stejně: nalezněte všechna prvočísla do zadané horní meze metodou Eratosthenova síta.
Principem Eratosthenova síta je to, že máme řadu čísel 2, 3, 4... až maximum. Vezmeme první číslo (2), jedná se o prvočíslo, a následně vyškrtáme všechny jeho násobky (4, 6, 8...). Vezmeme další nevyškrtnuté číslo v pořadí - 3. Opět vyškrtneme všechny jeho násobky (6, 9, 12...) a pokračujeme dalším nevyškrtnutým číslem (5, následně 7 atd.). Končíme u čísla, které je rovno odmocnině ze zadaného maxima.
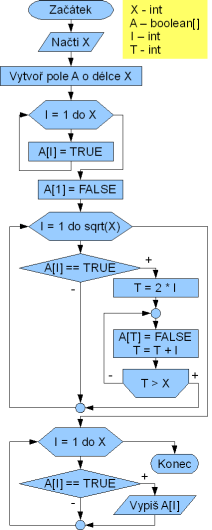
Pro vyškrtávání čísel si vytvoříme pole a protože nám stačí hodnota "vyškrtnuto/nevyškrtnuto", tak to bude pole binárních hodnot (boolean). Index do pole budou ona čísla, která bude vyškrtávat. Vyškrtnutá čísla budeme označovat jako false, takže si musíme všechny "šuplíčky" pole inicializovat napřed na true. A dále máme pole indexované od 1 a to není prvočíslo, takže číslo 1 (na indexu 1) vyškrtneme před samotným hledáním prvočísel.
Výsledný vývojový diagram můžete vidět na obrázku. Základem metody Eratosthenova síta jsou dva cykly - vnější s konečným počtem opakování a vnitřní s podmínkou na konci. Prvním procházíme čísla od 2 do odmocniny z maxima a hledáme nevyškrtnutá čísla. Druhým cyklem procházíme a vyškrtáváme násobky nalezeného nevyškrtnutého čísla - prvočísla, a to až do maxima. Cyklem na konci nalezená prvočísla vypíšeme.
Tím dnešní díl zakončíme. Příště se poprvé podíváme na důležitou disciplínu - třídění.
 TIP: Přetáhni ikonu na hlavní panel pro připnutí webu
TIP: Přetáhni ikonu na hlavní panel pro připnutí webu






