TIP: Přetáhni ikonu na hlavní panel pro připnutí webu
V minulém díle jsem snad dostatečně vychválil třídění, takže nezbývá než si ukázat první tři algoritmy, kterým můžeme dát nálepku: "ty jednodušší" - Select sort, Insert sort a Bubble sort. Součástí je samozřejmě implementace vývojovými diagramy.
Selection sort
Nebo také zkraceně SelectSort je asi nejjednodušší třídicí algoritmus. Jeho principem je najít v prohledávaném rozsahu 1 až N (kde N je počet šuplíčků pole) nejmenší číslo a zaměnit jej s prvním prvkem (šuplíčkem) v tomto poli. Následně se posune rozsah prohledání na 2 až N a provede se to samé atd. až do rozsahu N-1 až N. Tímto způsobem postupně setřídíme pole.
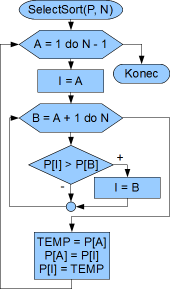
Vývojový diagram je vidět na obrázku. Už z popisu je jasné, že budeme používat cykly s daným počtem opakování. Potřebujeme měnit počátek rozsahu v rozmezí 1 až N-1 a použijeme na to první (vnější) cyklus (index I). Druhým (vnitřním) cyklem budeme procházet jednotlivé šuplíčky pole od I+1 do N (index J), porovnávat je s prvním v daném rozsahu (na indexu I) a hledat nejmenší číslo, od kterého si uložíme index.
Po skončení vnitřního cyklu se zamění hodnota mezi šuplíčkem na indexu I a na indexu, kde byla nalezená
nejmenší hodnota.
Výhodou SelectSortu, stejně jako všech dnes ukazovaných algoritmů na třídění, je jeho jednoduchost.
Nevýhoda je také stejná jako u všech ostatních, a to ta, že je pomalý a existují rychlejší algoritmy, které si ukážeme příště.
Insertion sort
Insertion sort (zkráceně InsertSort) je další z jednoduchých třídicích algoritmů. Opět máme na začátku nesetříděné pole v rozsahu 1 až N a principem InsertSort je postupné vkládání nesetříděných prvků do již setříděné části na správné místo, takže opět dostaneme setříděnou oblast, ale o jeden prvek větší.
Celé třídění začne od prvního prvku (šuplíčku) pole. Ten je samozřejmě seřazen (pole o jednom prvku je vždy seřazeno :)). Vezmeme další prvek a tyto dva prvky seřadíme, abychom dostali setříděnou posloupnost. Seřazení provedeme vložením prvku na správné místo (do správného šuplíčku) do již setříděné části pole (v druhém kroku zařazujeme prvek do setříděného jednoprvkového pole, ve třetím do dvouprvkového atd.). Vložení na správné místo může znamenat i to, že prvky již setříděného pole musíme posunout - udělat novému prvku místo v tom správném šuplíčku. A takto postupujeme dále, tj. vezmeme 3. (4., 5...) prvek pole a opět z prvních 3 (4, 5...) šuplíčků vytvoříme setříděné pole.
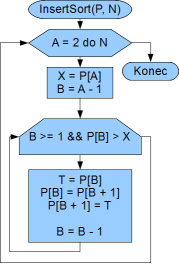
Vývojový diagram je na obrázku. Opět se algoritmus skládá ze dvou cyklů. První (vnější) je cyklus s daným počtem opakování, kterým postupně projdeme celé pole, resp. index tohoto pole ukazuje na první ještě nesetříděný prvek pole. Vnitřní cyklus je s podmínkou na začátku a tímto cyklem zařazujeme nový prvek do již setříděného pole.
Princip zařazování je následující: vezmeme šuplíček na právě kontrolovaném indexu. Otestujeme, jestli nejsme na kraji pole (index šuplíčku 1) nebo jestli vedle není menší číslo. Pokud je jedna z těchto podmínek splněná, tak končíme zařazování, protože jsme již na kraji pole nebo vedlejší šuplíček obsahuje menší číslo, tj. má zařazeno. Pokud tomu tak není, tak šuplíček s vedlejším prohodíme (jejich hodnoty) a index našeho šuplíčku zmenšíme o 1. A opět provedem test v cyklu s podmínkou na začátku.
Tento algoritmus je ze všech pomalých asi nejrychlejší (samozřejmě myšleno na průměrném vzorku). Další výhodou tohoto algoritmu je možnost použití jako tzv. online algoritmu, tj. lze třídit i data, která postupně přicházejí na vstupu (nejsou potřeba všechna data před začátkem třídění).
Bubble sort
Bublinkové třídění (bubble sort) je poslední z jednoduchých algoritmů na třídění, který si v tomto díle ukážeme. Jeho princip je opět jednoduchý - při procházení pole se porovnávají dva sousední šuplíčky a pokud nejsou ve správném pořadí (tj. v šuplíčku s nižším indexem je větší hodnota), tak se provede záměna hodnot v těchto dvou šuplíčcích. Pole se prochází tak dlouho, dokud se provádí nějaká záměna. Ve chvíli, kdy se při průchodu celým polem neprovede žádná záměna, je pole setříděné.
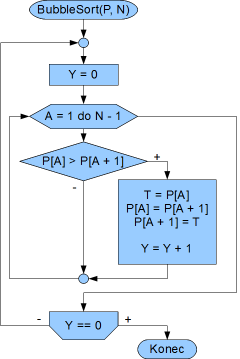
Vývojový diagram opět vidíte na obrázku. Stejně jako v předchozích příkladech jsou základem dva cykly. Vnější cyklus je s podmínkou na konci, kde testujeme, jestli se provedla nějaká záměna (počet změn si ukládáme do proměnné Y). Ve vnitřním cyklu s daným počtem opakování se prochází celé pole (do N-1), testují se sousední šuplíčky a případně se zaměňuje jejich obsah (a počítá počet změn).
Opět se jedná o jednoduchý, ale pomalý algoritmus, který má výhodu ještě v tom, že rychleji pracuje s poli, která jsou již částečně setříděná.
Jak již bylo řečeno, příště si ukážeme rychlejší a efektivnější algoritmy třídění.
