Řešíme zdrojový kód – algoritmus násobení

V článku budeme tak trochu vynalézat kolo. Ukážeme si zajímavý postup odvození algoritmu celočíselného násobení. Postup a tipy mohou být inspirací čtenáři, tréningem logického myšlení a věřím že i zábavou.

Pro násobení dvou přirozených čísel platí:

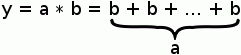
Totéž zapíšu v kódu, nejlépe se zde hodí přes cyklus for:

y = 0;
for (i = 0; i < a; i++) {
    y += b;	 
}

Tento kód násobí přirozená čísla včetně nuly, jinými slovy celá nezáporná čísla. Násobení celých čísel, z nichž alespoň jedno je záporné, je pro úplnost uvedeno ke konci článku rozšířením odvozeného kódu i na záporná čísla.

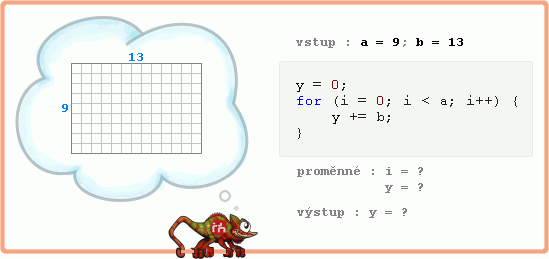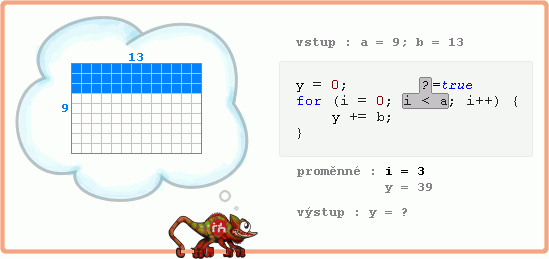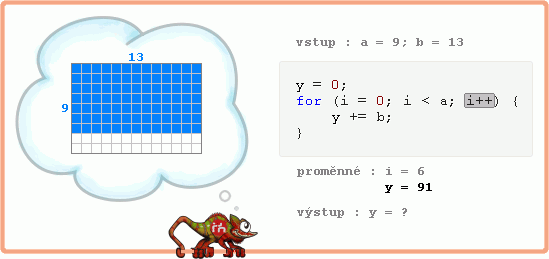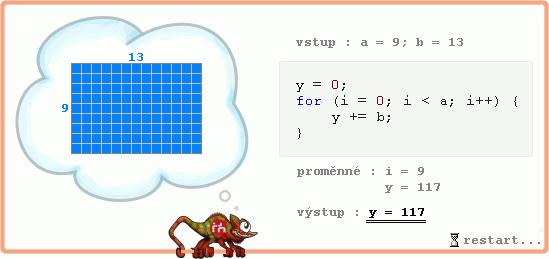
Zapsal jsem zadání do formy výchozího kódu, ale je to zoufale pomalý algoritmus násobení.
Nevadí, jeho výrazné urychlení je předmětem následujícího textu.

Poznámka:
Nedefinuju typ proměnných a, b, i, y. Bylo by to překážkou obecnosti. V průběhu odvození předpokládám, že pro jakýkoli vstup a hodnoty celých čísel ve všech místech kódu existuje vhodná (abstraktní) implementace, schopná proměnné uchovávat a operace s nimi provádět bez přetečení. Tedy navzdory tomu, že nejsme schopni držet v paměti celá čísla od mínus nekonečna do nekonečna, je možné pro jakýkoli vstup průběžně „držet hodnoty“ čísel, jež se „za běhu objeví“. Podrobněji k tomu viz můj delší příspěvek v názorech k článku Řešíme zdrojový kód – vztahy a pravidla.

Pomůcky pro řešení

Užitečnou pomůckou při úpravách cyklu je zkusit cyklus rozbalit, stačí pro pár průchodů. U uvedeného kódu je to snadné:

y += b;
y += b;
y += b;
y += b;
.
.
.

Můžu spojit dva průchody cyklu do jednoho. Snížím tím původní počet opakování cyklu na polovinu:

y += 2*b;
y += 2*b;
.
.
.

Řešení kódu

Poznámka:
Při každé následující úpravě kódu je výsledná funkce kódu po úpravě stejná jako funkce kódu před úpravou, tj. budu provádět ekvivalentní úpravy kódu. Nevypisuju v průběhu řešení na začátku kódů inicializaci y = 0;, to všude zůstává.

Úpravu naznačenou výše provedu ve výchozím kódu. Počet opakování cyklu vydělím dvěma a tělo cyklu naopak opakuju dvakrát. Musím přitom ošetřit případ, kdy je zbytek po celočíselném dělení dvěma nenulový a je třeba původní tělo cyklu provést ještě jednou:

for (i = 0; i < a / 2; i++) {
    y += 2 * b; // y += b; y += b;	 
}
if (a % 2 != 0) y += b;

Stejné „dělení cyklu“ na polovinu provedu znovu:

for (i = 0; i < a/2 / 2; i++) {
    y += 2 * 2*b; // y += 2*b; y += 2*b;	 
}
if (a/2 % 2 != 0) y += 2*b;
if (a   % 2 != 0) y += b;

A ještě jednou:

for (i = 0; i < a/2/2 / 2; i++) {
    y += 2 * 2*2*b; // y += 2*2*b; y += 2*2*b;	 
}
if (a/2/2 % 2 != 0) y += 2*2*b;
if (a/2   % 2 != 0) y += 2*b;
if (a     % 2 != 0) y += b;

S každou takovou úpravou přibývá pod cyklem jeden nový řádek kódu. Počet opakování cyklu naopak rychle klesá (a/2, a/4, a/8, …). Budu-li pokračovat ve stejných úpravách, dojde pro každou vstupní hodnotu proměnné a dříve či později k tomu, že výraz a / 2^N v podmínce cyklu bude roven nule a podmínka pokračování cyklu i < a / 2^N nebude splněna ani pro i = 0. Od okamžiku, kdy k tomu dojde, se tělo cyklu nevykoná už ani jednou. Proto je původní cyklus zbytečný, pryč s ním:

.
. 
.   
if (a/2/2 % 2 != 0) y += 2*2*b;
if (a/2   % 2 != 0) y += 2*b;
if (a     % 2 != 0) y += b;

V celém kódu se mění jen proměnná y, jejíž změna závisí na proměnných a, b, které se nemění, a platí: y + m + n = y + n + m (m, n – libovolná čísla). Proto můžu obrátit pořadí podmínek:

if (a     % 2 != 0) y += b;
if (a/2   % 2 != 0) y += 2*b;
if (a/2/2 % 2 != 0) y += 2*2*b;
.
. 
.

Nyní trochu obecněji využiju princip popisovaný v úvodním článku. Každý řádek je možné nahradit za if (d % 2 != 0) y += e;, kde výchozí hodnoty d = a, e = b. Funkce zůstane zachována, když se mezi řádky provede d /= 2; a e *= 2. Pomocné proměnné d, e můžu rovnou zase zpátky přejmenovat na a, b:

if (a % 2 != 0) y += b; 
a /= 2;
b *= 2;

if (a % 2 != 0) y += b;
a /= 2;
b *= 2;

if (a % 2 != 0) y += b;
a /= 2;
b *= 2;

.
.
.

V kódu je zatím neznámý počet opakujících se stejných trojic řádku. S každou trojicí se proměnná a celočíselně dělí dvěma, v určitém okamžiku už bude nulová a zůstane nulová, protože 0/2 = 0. Když má proměnná a nulovou hodnotu, je test a % 2 != 0 nepravda a proměnná y se už nikdy nezmění, proto další trojici řádků už pak netřeba provádět (a doplním zpátky vynechávanou inicializaci proměnné y):

y = 0;
while (a != 0) {
    if (a % 2 != 0) y += b;
    a /= 2;
    b *= 2;
}

= Výsledný algoritmus, asymptoticky rychlejší než původní. Jde o variantu Shift-Add algoritmu, často užívaného algoritmu násobení. I dnes najde praktické využití třeba na některých jednočipech, které nemají přímo instrukci pro násobení.

Finální optimalizace

Násobení a dělení dvěma jsou jednoduché operace ekvivalentní bitovým posunům. Test nenulovosti zbytku po dělení dvěma je ekvivalentní maskování nejnižšího bitu proměnné a:

y = 0;
while (a != 0) {
    if (a & 1) y += b;
    a >>= 1;
    b <<= 1;
}

Poznámka:
S tímto algoritmem také souvisí počítání v binární soustavě.

Příklad implementace

Užitím odvozeného algoritmu můžu napsat rutinu pro násobení 16bitových čísel. Mohla by vypadat třeba takto:

unsigned long umul16(unsigned short a, unsigned short b)
{
    if (a > b) swap(a,b);
    unsigned long y = 0;
    unsigned long c = b;
    while (a != 0) {
        if (a & 1) y += c;
        a >>= 1;
        c <<= 1;
    }

    return y;    		
}

V průběhu odvození jsem nedefinoval, jakého rozsahu jsou proměnné. Algoritmus samotný funguje obecně pro libovolnou velikost proměnných. Při implementaci se ale musí dát pozor na možné přetečení. Tady zrovna bylo nutné použít dvojnásobnou šířku pro hodnotu proměnné b (nahrazeno za c), protože se bitově posouvá doleva a docházelo by ke ztrátě vysunutých bitů.

Násobení čísel se znaménkem

Samotná absolutní hodnota výsledku násobení čísel se znaménkem je stejná jako výsledek u násobení bez znamének. Výsledné znaménko při násobení dvou čísel se znaménkem je dáno tabulkou:

Znaménko čísla je v podstatě k číslu přidaný jeden bit informace navíc, nejčastěji je tento bit přímo uložen v nejvyšším bitu čísla jako „1“ pro „-“. Můžu tu tabulku zapsat takto:

Tato tabulka představuje logickou funkci exkluzivní disjunkce (XOR). Jinak se ji v případě dvou vstupů říká také nonekvivalence, protože jednička je na výstupu jen tehdy, jsou-li hodnoty vstupů rozdílné. Proto násobení čísel se znaménkem můžu provést tak, že zjistím zdali mají vstupní čísla rozdílná znaménka, tato znaménka odstraním, provedu násobení čísel bez znamének a nakonec u výsledku změním znaménko na opačné, když vstupní čísla mají znaménka rozdílná. (Také bych mohl použít operátor  ^)

Příklad implementace násobení se znaménkem

long imul16(short a, short b)
{
    unsigned long y = 0;
    unsigned long c = abs(a);
    unsigned long d = abs(b);

    if (c > d) swap(c, d);

    while (c != 0) {
        if (c & 1) y += d;
        c >>= 1;
        d <<= 1;
    }
    
    if ( (a < 0) != (b < 0) ) {
        return - (long) y;
    } else {
        return (long) y;
    }
}

Poznámka:
Miloslav Ponkrác v diskusi pod článkem dobře dodává, že zjištění znaménka se v praxi dělá rychleji než v příkladu předchozího kódu, tedy místo :

  if ( (a < 0) != (b < 0) ) { ...

se spíše používá:

  if ((a ^ b) < 0) { ...

Tím se XORují se všechny bity a, b. Znaménko je jeden z nich a porovnáním s nulou testuje hodnotu znaménkového bitu ve výsledku toho XOR.

Závěr

Z pomalého algoritmu násobení na začátku máme rychlý algoritmus na konci. Mezitím jsem provedl pár ekvivalentních logických úprav. Postup samotný není všespasitelný, ale v nemálo případech může být užitečný a účinný.

Dobré na podobném postupu je také to, že celý průběh řešení je přesně dokumentován. Každý se tak může přesvědčit a snadno pochopit přímo v kontextu jazyka, kterému jako programátor přirozeně rozumí, jak se postupně došlo k výsledku.

Autorem postavičky CMYKa, zdejšího maskota koukajícího v obrázcích, je Zbyněk Molnár.