Názory ke článku Středoškolská fyzika, začátek – co je třeba znát? – Programujte.com

Zdravím tě Jimmy :)

Dobrá práce. Těším se na další díly.

Jenom malá poznámka: podle mých pocitů a zkušeností je "vědecká" fyzika (např. na matfyzu) podstatně méně názorná než ta středoškolská, takže bych řekl, že té matematiky je tam ještě o dost víc než jen polovina. :-(

Prosím, důkladně zkontroluj znaménka u prvních dvou příkladů a potvrď, že tam nejsou chyby. dík.

#3 rp
Při předělávání jsem musel hloupě přehodit znaménko u a), díky za upozornění. Prozatím dám příklad sem do komentářů a časem to upravím i ve článku.

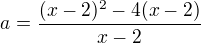
a v příkladě b) se mi nezdá, že je špatně znaménko, dal jsem tam schválně mocninu, aby se nedal čitatel rozložit, ale toho "mechanického matematika" by napadlo při x a 8 to rozložit podle x^3 +- a^3. :-) Ten druhý vyjde ošklivě. :-)

Za ten první se vážně omlouvám.

Ahoj Jimy, supr. Těším se na další díly.

Musím pochválit i češtinu (až na výraz Pracování s jednotkami). Tak dobrá se totiž na internetu moc nevidí.

Neškodilo by napsat, že delta je rozdíl, změna měřené veličiny, např. polohy tělesa na začátku měření a na konci měření.

Pro zájemce o fyziku (tedy nestudenty) bude stačit názorné vysvětlení integrálu, jak to chápou fyzici, a ukázat to na rychlosti a dráze: ujetá dráha je součet malinkých useků dráhy ujetých za časové pididobičky krát pididobička, na grafu součet úplně tenounlinkých obdélníčků. Prostě moc jemný součet něčeho. Uf

#5 ufak
Za češtinu děkuji, i když vidím občas někdy i překlepy, kterých si ani korektoři nevšimli - proto chci příspěvek upravit až déle, abych to udělal všechno najednou.

S tou deltou a rozdílem máš pravdu, doplním tam někam poznámku. -)

A názorné vysvětlení integrálu se mi tady moc ukazovat nechce, chci tady mít čistě to "matematicky jsme k tomu došli takhle". Názorné vysvětlení integrálu si plánuji do článku "základy integrálního počtu", které jsme se učili na gymnáziu ve třeťáku a začátku čtvrťáku - připravuji i něco "Matematické vysvětlivky pro kurz fyziky", kde bude výklad právě téhle matematiky, kterou já používám.

A té pochvaly s češtinou si velmi vážím, je to jedna z mála věcí, které dávám vyšší prioritu než obecné znalosti matematiky a fyziky. Leč tyhle dvě vědy miluji, být společensky na úrovni znamená mít všeobecné vzdělání a umět se vyjadřovat - jinak řečeno, beru to tak, že jsi mi právě řekl, že nejsem společenský idiot, proto si toho cením. :) A to, že jsi vytkl "Pracování s jednotkami" jen dokazuje, že stále mám co zlepšovat. :)

#6 found
ahoj. To Pracování s jednotkami vypadá, jako kdyby to přeložil googlík... :-) čao

#7 ufak
Tak je do budoucna, jak s tím "nakládat"? :) Mě zrovna nenapadá vhodnější slovo, tak se omlouvám za svou omezenou slovní zásobu. :-)

#7 ufak #8 found
Já bych to pracování s různými věcmi (i nevěcmi) neviděl tak černě :)

Pracuje se s výrazy, pracuje se s veličinami, pracuje se s nástroji... S čistým svědomím bych nechal Jimmyho pracovat i s jednotkami ;)

#9 deedx
dyk jo, stačí napsat Práce s .... Nebude to tak anglicky.

#4 found
Ok. U druhého příkladu zkus (x^2-8) změnit na (x^2+8). Ne že by se vzorce měly předělávat, aby lépe vycházely :) Ale v ukázkových příkladech to může více motivovat, co myslíš? Když budou vycházet obludy, těžko vysvětlíme, že měla úprava nějaký význam. Když vyjde významné zjednodušení, vysvětlíme snadněji, že má úprava smysl.

Jak to bude s uveřejněním výsledků? Plánuješ nějaký rozbor?

#11 rp
No, příklady se dají odevzdávat, takže pro toho, kdo je odevzdá, řeknu, jestli je to dobře nebo ne a kde případně udělal chybu. :) Výsledky bych mohl dát do nějakého speciálního dílu po dokončení kurzu :)