
Google Code Jam pokračuje třetím kolem.
Velikost kapes
 Zadání: Máme zadaný tvar pravoúhelníka (všechny souřadnice jsou celočíselné) a naším úkolem je zjistit velikost jeho „kapes“. Bod v kapse je definován tím, že jednak neleží uvnitř pravoúhelníka a jednak existuje hranice vlevo i vpravo nebo nahoře i dole. Naším úkolem je zjistit velikost těchto kapes. Řešení
Zadání: Máme zadaný tvar pravoúhelníka (všechny souřadnice jsou celočíselné) a naším úkolem je zjistit velikost jeho „kapes“. Bod v kapse je definován tím, že jednak neleží uvnitř pravoúhelníka a jednak existuje hranice vlevo i vpravo nebo nahoře i dole. Naším úkolem je zjistit velikost těchto kapes. Řešení
K řešení se dá přistoupit několika způsoby. V první řadě bychom velikost kapes mohli přesně spočítat, to by ale bylo poměrně pracné. Proto můžeme využít faktu, že jsou souřadnice celočíselné, a postupně vyzkoušet všechny body. Pokud má bod v libovolném kolmém směru nula průsečíků, tak je venku, pokud má lichý počet průsečíků, tak je uvnitř, jinak je v kapse.
/** Určení velikosti kapes pravoúhelníku
* @param array $xs všechny body na souřadnici X ve tvaru array($x => array($y, ...), ...)
* @param array $ys všechny body na souřadnici Y ve tvaru array($y => array($x, ...), ...)
* @return int velikost kapes
*/
function pockets($xs, $ys) {
ksort($xs);
ksort($ys);
$return = 0;
foreach ($xs as $i => $x) {
sort($x);
$crosses_x = 0;
foreach ($ys as $j => $y) {
if (isset($x[$crosses_x]) && $x[$crosses_x] <= $j) {
$crosses_x++;
}
if ($crosses_x % 2 == 0) {
if ($crosses_x != 0 && $crosses_x != count($x)) {
$return++;
} else {
$crosses_y = 0;
foreach ($y as $val) {
if ($val <= $i) {
$crosses_y++;
}
}
if ($crosses_y != 0 && $crosses_y != count($y)) {
$return++;
}
}
}
}
}
return $return;
}Postupně procházíme všechny body a do proměnné $crosses_x si načítáme počet průsečíků na souřadnici X. Když je nulový nebo maximální, tak musíme prozkoumat ještě souřadnici Y, když je lichý, tak jsme uvnitř, jinak jsme v kapse.
Kód by se dal zoptimalizovat tím, že by se postupně načítaly i souřadnice Y (do pole $crosses_ys). Další optimalizace by spočívala v tom, že při nenulovém počtu průsečíků X by se skočilo až na další průsečík a započítaly by se všechny body najednou.
Portál
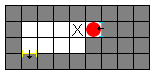 Zadání: Kdekoliv v bludišti a všude kolem něj jsou rozmístěny zdi (všechny souřadnice jsou celočíselné). Zadaná je naše pozice v tomto bludišti a pozice dortu, ke kterému se chceme dostat. Kromě běžných pohybů můžeme na zdech vytvářet portály dvou druhů – žlutý a modrý (když vytvoříme už existující portál, tak původní zmizí). Vstupem do žlutého portálu se objevíme v modrém a naopak. Naším úkolem je zjistit minimální počet pohybů, kterými se můžeme dostat k dortu. Za pohyb se považuje posun nahoru, dolů, doleva nebo doprava a vstup do portálu. Naopak vytvoření portálu je zdarma. Řešení
Zadání: Kdekoliv v bludišti a všude kolem něj jsou rozmístěny zdi (všechny souřadnice jsou celočíselné). Zadaná je naše pozice v tomto bludišti a pozice dortu, ke kterému se chceme dostat. Kromě běžných pohybů můžeme na zdech vytvářet portály dvou druhů – žlutý a modrý (když vytvoříme už existující portál, tak původní zmizí). Vstupem do žlutého portálu se objevíme v modrém a naopak. Naším úkolem je zjistit minimální počet pohybů, kterými se můžeme dostat k dortu. Za pohyb se považuje posun nahoru, dolů, doleva nebo doprava a vstup do portálu. Naopak vytvoření portálu je zdarma. Řešení
Řešení: Vyzkoušíme všechny možnosti průchodu. Prohledávat budeme do šířky, protože chceme nalézt minimální možný počet pohybů:
function portal($maze, $y, $x) {
$visited = array();
$explore = array(array($y, $x, null, null, null, null));
for ($depth=0; $explore; $depth++) {
for ($type=0; $type < 2; $type++) {
foreach ($explore as $val) {
list($y, $x, $y1, $x1, $y2, $x2) = $val;
if ($maze[$y][$x] === false) {
return $depth;
}
foreach (array(array(-1, 0), array(0, 1), array(1, 0), array(0, -1)) as $val) {
list($j, $i) = $val;
$n = $y;
$m = $x;
while (!$maze[$n+$j][$m+$i]) {
$n += $j;
$m += $i;
}
if (($n !== $y1 || $m !== $x1) && ($n !== $y2 || $m !== $x2)) {
if ($type) {
portal_visit($explore, $visited, $y, $x, $y1, $x1, $n, $m);
} else {
portal_visit($explore, $visited, $y, $x, $n, $m, $y2, $x2);
}
}
}
}
}
$explore2 = array();
foreach ($explore as $val) {
list($y, $x, $y1, $x1, $y2, $x2) = $val;
if (isset($y1) && isset($y2)) {
if ($y == $y1 && $x == $x1) {
portal_visit($explore2, $visited, $y2, $x2, $y1, $x1, $y2, $x2);
} elseif ($y == $y2 && $x == $x2) {
portal_visit($explore2, $visited, $y1, $x1, $y1, $x1, $y2, $x2);
}
foreach (array(array($y-1, $x), array($y, $x+1), array($y+1, $x), array($y, $x-1)) as $val) {
list($n, $m) = $val;
if (!$maze[$n][$m]) {
portal_visit($explore2, $visited, $n, $m, $y1, $x1, $y2, $x2);
}
}
}
}
$explore = $explore2;
}
return "THE CAKE IS A LIE";
}Kód není zrovna vrcholem elegance, což je způsobeno především tím, že vytvoření portálu není považováno za pohyb. Proto musíme nejdřív zkusit vytvořit všechny kombinace portálů a teprve potom můžeme začít zkoušet pohyby a vstup do portálů. Pro přidání dalšího prvku pro zkoumání se používá pomocná funkce:
function portal_visit(&$explore, &$visited, $y, $x, $y1, $x1, $y2, $x2) {
if (!isset($visited["$y,$x $y1,$x1 $y2,$x2"])) {
$visited["$y,$x $y1,$x1 $y2,$x2"] = true;
$explore[] = array($y, $x, $y1, $x1, $y2, $x2);
}
}Samozřejmě už nezkoušíme stavy, které jsme dříve prozkoumali. Stav je definován naší pozicí v bludišti a místem východů obou portálů.
Bez podvádění
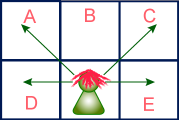 Zadání: Učebna je plná židlí, některé z nich jsou ale rozbité. Naším úkolem je posadit na tyto židle co nejvíc studentů tak, aby nemohli podvádět při písemce. Student totiž vidí doleva a doprava ve své a předchozí řadě. Řešení
Zadání: Učebna je plná židlí, některé z nich jsou ale rozbité. Naším úkolem je posadit na tyto židle co nejvíc studentů tak, aby nemohli podvádět při písemce. Student totiž vidí doleva a doprava ve své a předchozí řadě. Řešení
Řešení: Vyzkoušíme všechny kombinace rozmístění židlí. Židle, ze kterých by se dalo opisovat, označujeme stejně, jako kdyby byly rozbité:
function classroom($m, $n, $broken, &$cache, $j=0, $i=0) {
$return = 0;
for (; $j < $m; $j++) {
for (; $i < $n; $i++) {
if (!isset($broken[$j][$i])) {
$broken1 = $broken;
$broken1[$j+1][$i-1] = true;
$broken1[$j+1][$i+1] = true;
$key = 0;
for ($k=2; $k <= $n; $k++) {
$key = 2*$key + (isset($broken1[$j + floor(($i+$k) / $n)][($i+$k) % $n]) ? 1 : 0);
}
if (!isset($cache[$j][$i][$key])) {
$cache[$j][$i][$key] = classroom($m, $n, $broken1, $cache, $j, $i+2);
}
$return = max($return, 1 + $cache[$j][$i][$key]);
}
}
$i = 0;
}
return $return;
}Vyzkoušené kombinace se stejně jako u Přepínání vyhledávačů ukládají do proměnné $cache. Kombinace je definovaná pozicí a přehledem nepoužitelných židlí v řadě pode mnou.
Tahy koněm
 Zadání: V levém horním rohu obrovské šachovnice stojí šachový kůň. Jeho cílem je dostat se do pravého dolního rohu. V každém tahu musí kůň postoupit k cíli (takže může skákat buď doprava a dolů nebo dolů a doprava). Na šachovnici jsou ale některá políčka rozbitá, takže na ně kůň nemůže stoupnout (může je ale přeskočit). Naším úkolem je spočítat počet možných cest, kterými se kůň k cíli může dostat, pokud jsou zadané rozměry šachovnice a pozice rozbitých políček. Protože výsledek může být obrovský, stačí vrátit zbytek po dělení číslem 10007. Řešení
Zadání: V levém horním rohu obrovské šachovnice stojí šachový kůň. Jeho cílem je dostat se do pravého dolního rohu. V každém tahu musí kůň postoupit k cíli (takže může skákat buď doprava a dolů nebo dolů a doprava). Na šachovnici jsou ale některá políčka rozbitá, takže na ně kůň nemůže stoupnout (může je ale přeskočit). Naším úkolem je spočítat počet možných cest, kterými se kůň k cíli může dostat, pokud jsou zadané rozměry šachovnice a pozice rozbitých políček. Protože výsledek může být obrovský, stačí vrátit zbytek po dělení číslem 10007. Řešení
Řešení: Pro malý vstup (rozměry šachovnice jsou maximálně 100×100) stačí vyzkoušet všechny možnosti. Opět se využívá dynamické programování:
function knight($h, $w, $rocks, &$cache) {
if (isset($rocks[$h][$w]) || $h >= 2*$w || $w >= 2*$h) {
return 0;
} elseif ($h == 1 && $w == 1) {
return 1;
}
if (!isset($cache[$h][$w])) {
$cache[$h][$w] = (knight($h-1, $w-2, $rocks, $cache) + knight($h-2, $w-1, $rocks, $cache)) % 10007;
}
return $cache[$h][$w];
}Pro velký vstup (rozměry šachovnice až 108×108, ale jen 10 špatných políček) by bylo potřeba problém řešit koncepčně odlišně. Bez rozbitých políček by se dal počet skoků vyjádřit jako kombinační číslo (m+n nad n), kde m je maximální počet skoků na šířku a n na výšku. Cesty vedoucí přes rozbité kameny bychom potom za použití stejného výpočtu odečetli. Z kombinačního čísla ale neumím rychle vypočítat zbytek po dělení (pro celočíselnou mocninu se dá použít funkce bcpowmod).
 TIP: Přetáhni ikonu na hlavní panel pro připnutí webu
TIP: Přetáhni ikonu na hlavní panel pro připnutí webu






