Vývojové diagramy - 3. díl

Než se začínající programátor vrhne na učení nějakého jazyka, měl by si osvojit techniku „myslet jako počítač“. Rozumí se tím umět problém rozdělit na jednotlivé krátké části, dílčí úseky, které ve výsledku budou tento problém řešit, neboli vytvořit algoritmus. Proces tvoření algoritmu se nazývá algoritmizace a vývojové diagramy jsou jedním z nástrojů pro jejich zápis.

Předchozí dva díly (první, druhý) byly věnovány vývojovým diagramům z obecného hlediska. Víme tedy, z čeho se takový vývojový diagram může skládat a jak mohou vypadat různé varianty větvení a cyklení. Ale je rozdíl v tom znát cestu a jít po ní… [Morfeus, film Matrix]. Následujících několik dílů bude věnováno řešení konkrétních problémům od jednoduchých po složitější.

Tento díl je věnován úplně těm nejjednodušším algoritmům, které obsahují pouze vstup od uživatele, zpracování (výpočet) a vypsání výsledku. Začneme používat tyto 4 značky:

• označení začátku/konce
• spojení
• vstup/výstup
• příkaz

Značka pro vstup je stejná jako značka pro výstup (společná značka pro vstupně-výstupní operace). Rozlišovat je budeme zápisem textu do značky.

Dost bylo úvodu a přejděme k praktickým ukázkám. Začneme tím nejjednodušším.

Ahoj světe

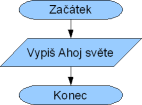
Témeř každá kniha nebo seriál o programování začíná aplikací typu „Hello World“. Tak ani my neuděláme výjimku a pro takovou aplikaci si vytvoříme vývojový diagram. Program je to velice jednoduchý, chceme pouze vypsat text na výstup, aby si ho uživatel mohl přečíst. K výpisu použijeme značku pro vstupně-výstupní operace s popisem činnosti.

„Ahoj světe“ je sice velmi hezký program, ale takových, které by pouze něco vypisovaly, je jako šafránu (pokud vůbec). Ostatní programy zpracovávají nějaká data a je v podstatě úplně jedno, jestli data zadává uživatel, čtou se ze souboru, jsou výsledkem komunikace, nebo jsou uložena v databázi. Všechny (s největší pravděpodobností) vývojové diagramy, které budou v rámci tohoto seriálu rozebrány, budou mít na vstupu načtení dat od uživatele, ale klidně by to mohlo být i načtení ze souboru nebo z databáze.

Sčítání dvou čísel

Zadáním úlohy je vytvořit algoritmus na sčítání dvou čísel. Každého, kdo začíná, tak určitě napadne otázka: jakých dvou čísel? Tím se dostaneme k jedné z vlastností, které musí každý navržený algoritmus splňovat, a to hromadnost. Hromadnost znamená, že algoritmus neslouží k řešení jedné úlohy (konkrétních dat), ale slouží k řešení celé skupiny úloh, které se od sebe liší jen vstupními daty.

Hromadnost – algoritmus neslouží k řešení jedné úlohy, ale k řešení celé skupiny úloh, které se od sebe liší jen vstupními daty.

Odpověď na otázku „součet jakých dvou čísel“ je tedy jednoduchá: libovolných dvou čísel. Tato libovolnost má samozřejmě svoje omezení daná požadavky na vstupní data (např. všechna celá čísla). Nebudeme tedy sčítat dvě konkrétní čísla (např. 5 + 8), ale dvě libovolná čísla, která reprezentujeme zástupným označením (jménem, např. číslo1 a číslo2). Hodnota takto označených čísel se může měnit, bude proměnná – odtud tedy název pro toto označení — proměnná.

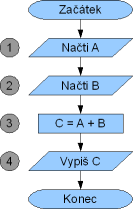
Sčítat budeme tedy dvě čísla, která načteme ze vstupu (zadá je uživatel) a budou zastoupena proměnnými. Následně je sečteme, výsledek opět uložíme do proměnné a vypíšeme. Tím je celý algoritmus hotov a můžeme ho zakreslit. Výsledný vývojový diagram obsahuje zadání prvního čísla (načte se a uloží do proměnné A) a druhého čísla (B). Následuje výpočet součtu, uložení výsledku do proměnné C a jejího následného vypsání.

Čísla vedle vývojového diagramu označují číslo kroku (označeny tak budou pouze vývojové diagramy v prvních několika dílech). Toto číslo použijeme v tabulce hodnot, která obsahuje hodnoty pro zvolenou sadu vstupních dat, a to z důvodu lepší názornosti. Tabulka hodnot se používá pro kontrolu správnosti algoritmu. Na obrázku si můžete prohlédnout tabulku pro zadané hodnoty 10 a 5 (včetně popisu).

A narážíme na další otázku začátečníků: a kde se ta čísla vezmou? Tato čísla simulují vstup od uživatele, jsou vybrána zcela náhodně a vybírá je ten, kdo bude tvořit algoritmus resp. vývojový diagram. Pokud se vám líbí třeba číslo 5, tak můžete do omrzení zadávat na vstupu číslo 5. Pro vyzkoušení algoritmu je ovšem velmi vhodné zadávat taková čísla (data), která budou testovat i tzv. mezní případy. V příštím díle si ukážeme, co takový mezní případ je a samozřejmě si pro něj vytvoříme i tabulku.

Násobení dvou čísel

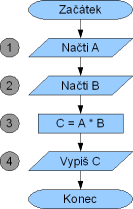
Zadáním úlohy je vytvořit algoritmus pro násobení dvou čísel. Opět tedy potřebujeme na vstupu dvě čísla, která vynásobíme a výsledek vypíšeme. Vstupem algoritmu budou dvě čísla a výstupem výsledek (jejich součin). Úloha je tedy v podstatě stejná jako v předchozím případě, a proto nebudeme na nic čekat a vývojový diagram pro tento algoritmus zakreslíme. Výsledný vývojový diagram se liší pouze v početním operátoru.

Tabulka hodnot zobrazuje obsah proměnných při zadání čísel 3 a 7. Čísla byla zvolena opět náhodně.

Výpočet objemu válcové nádoby

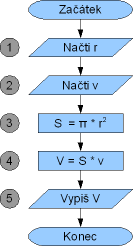
Zadáním úlohy je vytvořit algoritmus na výpočet objemu válcové nádoby. K výpočtu objemu válcové nádoby použijeme vzorec V = πr²v, kde r je poloměr podstavy a v je výška válce. K výpočtu tedy potřebujeme poloměr podstavy a výšku válce, které budou vstupem algoritmu. Výstupem algoritmu bude objem válce. Potřebujeme tedy zadat obě hodnoty, vypočítat objem a vypsat ho. Úloha je tedy opět velmi podobná těm předchozím. My si v ní z cvičných důvodů ovšem uděláme jednu změnu, a to takovou, že výpočet provedeme s mezivýsledkem. Nejprve si spočítáme obsah podstavy a následně celkový objem.

Tabulka hodnot zobrazuje obsah proměnných v jednotlivých krocích při zadání čísel 1 a 2. Čísla byla zvolena opět náhodně.

V  příštím díle si přidáme podmínku, která nám umožní větvit program a tvořit složitější konstrukce.